今年もよろしくお願いします。 長年の課題で今年こそ解決したい問題について書きます。
この記事のポイント
- 河川流一次元計算は独特の難しさがある
- 数値解法によって水位に大差が生じる
モチベーション
- 一次元浅水流方程式(Saint-Venant 方程式)を実河川の計算用に拡張した断面平均一次元浅水流方程式の計算方法について改めて整理しました。
実河川の一次元計算の独特の難しさ
横断面形状の取り扱い方法
computational-sediment-hyd.hatenablog.jp
水深を陽的に扱えない
断面平均一次元浅水流方程式は次のとおりですが、
ポイントは、水深、河床高が定義しづらいため、左辺第3項のを
のように水深(圧力項)と河床高(重力項)に分離できないことです。
そのため、特性曲線の考え方が使いづらくなります。一方、ドライベッド(河床勾配あり)はこの式形のほうが解きやすくなります。
Δxを任意に取れない
実河川では縦断方向200m間隔で横断測量を行うこと一般的です。河川地形は複雑で幾何補間が難しいため、測量間隔を数値計算のΔxと使うことが多い。
計算スキーム
以下の3スキームを比較する。
不定流計算のスキームを選ぶ基準は、1). 急流河川でも解けること、2). ロバストであることです。
特に私のような立場では、一つのモデルで何十河川も計算するので、2).ロバスト性は重要になります。
一応ですが、計算コードはこちら
参考文献
- 1.「9.1.5 Upwind flux scheme」参照
リンク
- 2.「【例題 2-9】常流・射流混在流れ」参照
リンク
テスト計算
計算条件
- 河床高は、平均河床勾配1/400で縦断方向200m間隔で地形データが存在するとしてその地点に-1から1の乱数を加えて実河川を模した河床形状を作った。
- 河幅は50mで一定とする。
- 縦断距離は10km
- 粗度係数は0.03とする。
計算結果
基本ケース
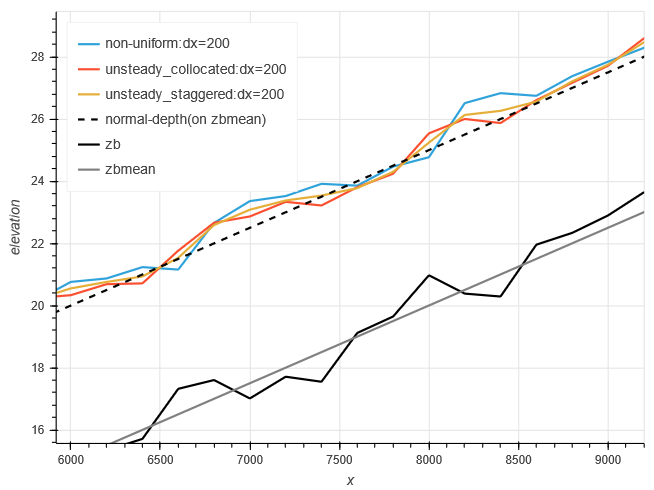
- 各計算スキームによる計算水位とフルード数と図化しました。
- 不定流は適当な初期値を与えて定常になるまで計算しています。
- 参考として平均河床での等流水深も示しています。
拡大図を見ると、
- 各スキームで最大1m程度の差が生じている。
- 不等流が最もシャープな水面形でその次は不定流:コロケート格子であり、不定流:スタッガードが最も滑らかになっている。
- 河床形状に対する水面形の応答が不等流と不定流でずれている。
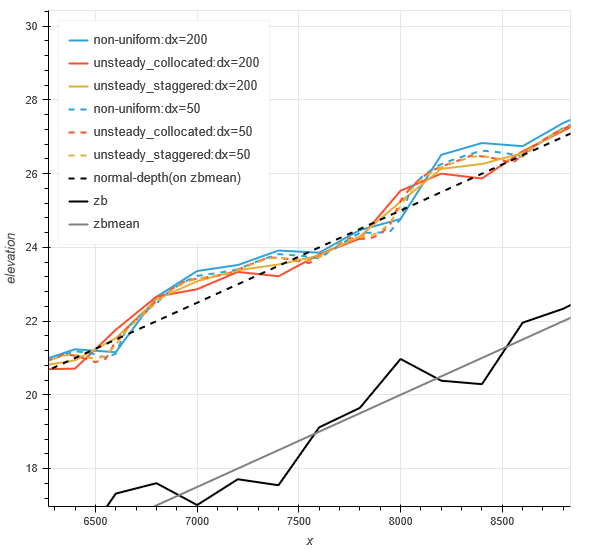
dxを50mに設定:内挿断面
- 前述の河床形状をもとにdxを200mから50mに変更するように内挿断面を設定した。
- 水面形の比較を示す。
拡大図を見ると、
- 各スキームの差はdx=200mの場合と比較して小さくなっている。
- この値が真値に近いとすると、dx=200mによる再現性は、
- 不等流は形状は真値に近いが水位が高い。
- 不定流は平均的な水位は真値に近い。
ゆるく考察
- 前述のとおり実河川の計算ではdxを任意にとることが難しいのでdx=200mで計算することを基本に考える。
- dx=200の不定流でもう少し高精度な(シャープな)水面形を計算したい。
- 汎用性を考えるとコロケート格子を使いたい。
- 以下(「6.4 コロケート格子・・・」の最後)によるとコロケート格子はスタッガード格子に比べて精度が低くなる。
リンク
- しかし、次の論文(森西ら)による定義点を適切に評価することによりその差は無くなると示されている。
https://www.jstage.jst.go.jp/article/kikaib1979/65/630/65_630_505/_pdf/-char/ja
- 今回の計算では、全体的な水面形のずれはほぼ無いため、局所的な運動量のバランスによって水面形の差が生じていると考えられる。
- 今後のテーマとして、コロケート格子で局所的な保存則を満たしたスキームの開発を考える。(多分陰解法になる気がします。)
GitHub
図化等の参考記事
- グラフの作成はHoloviewsを使用
computational-sediment-hyd.hatenablog.jp
- はてブロへのhtmlグラフの埋め込み