Manningの粗度係数を再考する - 趣味で計算流砂水理 Computational Sediment Hydraulics for Fun Learning

頭の整理に書いてみました。ご指摘があれば

Manningの公式の概要
Manningの公式への水理学的な意味付け
沖積河川の河床抵抗
河床波の変化を考慮した河床抵抗の評価方法
岸・黒木の方法による河床抵抗の評価
岸・黒木の方法の課題
- 河床波の遷移の履歴
- 河床波の形状抵抗の直接評価
参考：流砂量評価における有効掃流力
参考図書
Github

Manningの公式の概要

Manningの公式は、Robert Manningによって提案された横断面内で平均化された流速 $V$ を示す実験公式であり、次式のように示される。

$\begin{align} V = \dfrac{1}{n}i_e^{1/2}R^{2/3} \end{align}$

ここで、 $n$ ：Manningの粗度係数（ $m^{-1/3} \cdot s$ ）、 $i_e$ ：エネルギー勾配、 $R$ ：径深（m）である。

本式は現在世界で最も使われている平均流速公式である。上式の実験定数はManningの粗度係数のみであるが次元を有しており定数として適切でない。それにもかかわらず、式形が非常に単純なため、実験水路から実河川まで様々な条件下での豊富な観測資料を元にManningの粗度係数は整理されている。そのため、容易に概略値を把握することが可能である。

例えば、Chowの「OPEN-CHANNEL HYDRAULICS」では水路条件を100種類以上に分類し、Manningの粗度係数を一般値を示している。¹

日本では「水理公式集(平成11年版)」²や「河川砂防技術基準(案)同解説調査編」³に次表のようにまとめられている。

「水理公式集(平成11年版)」

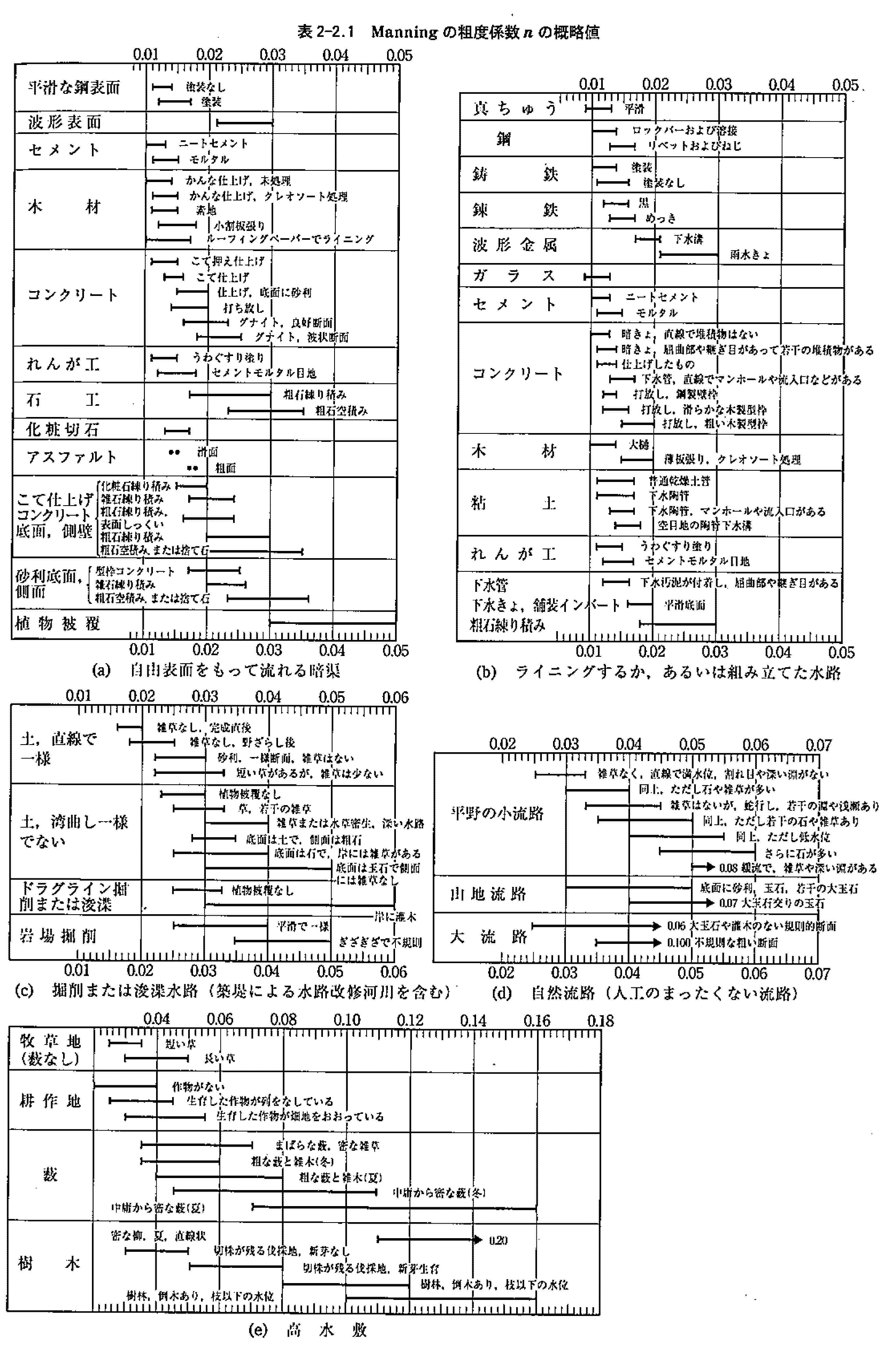
「河川砂防技術基準(案)同解説調査編」

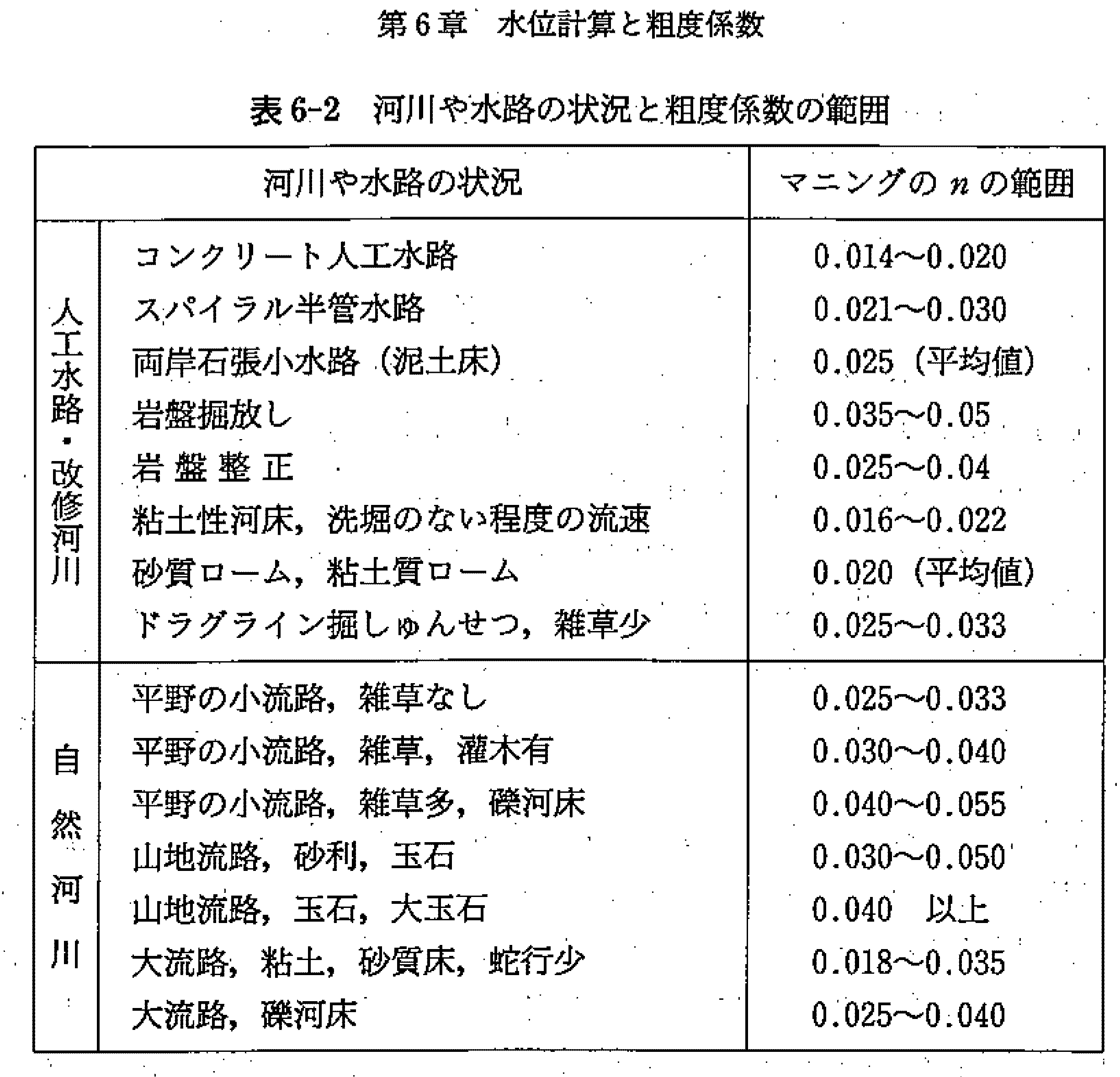
Manningの公式への水理学的な意味付け

流速係数 $\phi=V/u_*$ をManningの公式を用いて整理すると次式となる。

$\begin{align} \phi &= \frac{V}{u_*} = \frac{k_s^{1/6}}{n \sqrt{g}} \left(\frac{R}{k_s} \right)^{1/6} \nonumber \end{align}$

ここに $k_s$ ：相当粗度(m)である。一方開水路完全粗面の対数則による流速係数は次式となる。

$\begin{align} \phi &= \frac{1}{\kappa}\log_e{\frac{h}{k}} - \frac{1}{\kappa} + C \end{align}$

両式より、 $\phi$ と $k_s^{1/6}/(n \sqrt{g})$ の関係を整理したものが次図の点線である。

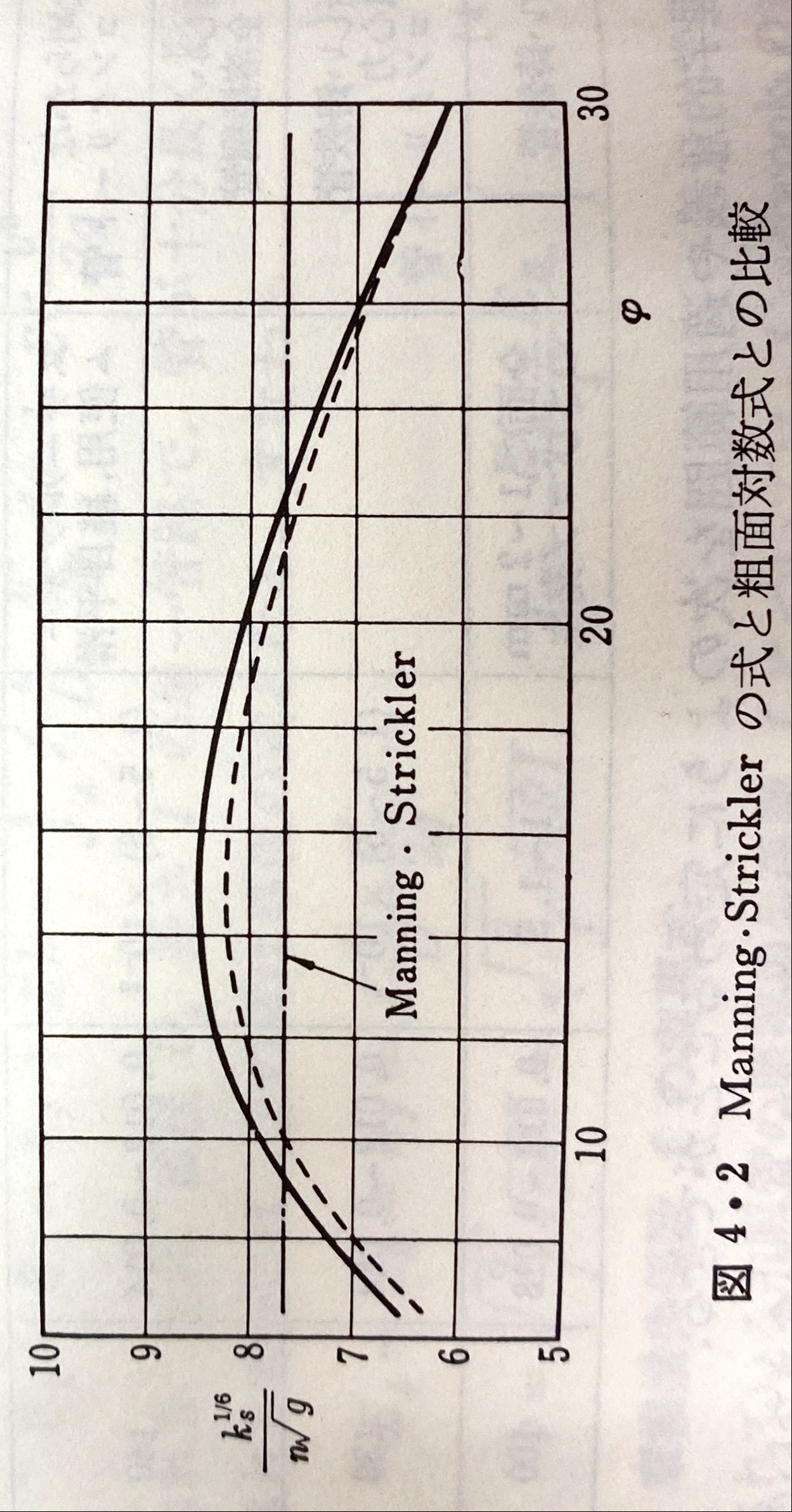
図　Manning・Stricklerの式と粗面対数則との比較⁴

管路や開水路では流速係数 $\phi$ は8～25程度であるため、 $k_s^{1/6}/(n \sqrt{g})$ は図中直線の一定値に近似できる。これより、流速係数は以下のように近似できる。

$\begin{align} \frac{k_s^{1/6}}{n \sqrt{g}} & \sim 7.66 \nonumber \\ \phi &= \frac{V}{u_*} = 7.66 \left(\frac{R}{k_s} \right)^{1/6} \end{align}$

これはManning・Stricklerの公式と呼ばれる。上記のように近似できることは実用上は径深によってManningの粗度係数が変わらないことを示している。今日では本式を使用することは少ないが、Manningの公式に水理学的な意味を与えた点で重要である。

沖積河川の河床抵抗

多くの沖積河川では河床上に河床波（小規模河床形態）が形成されている。河床波とは砂漣、砂堆、反砂堆等の水深スケールの河床形状を示して、日本土木学会水理委員会によると次表のように分類される。⁵ また、Simonsはより詳細な分類を示している。⁶

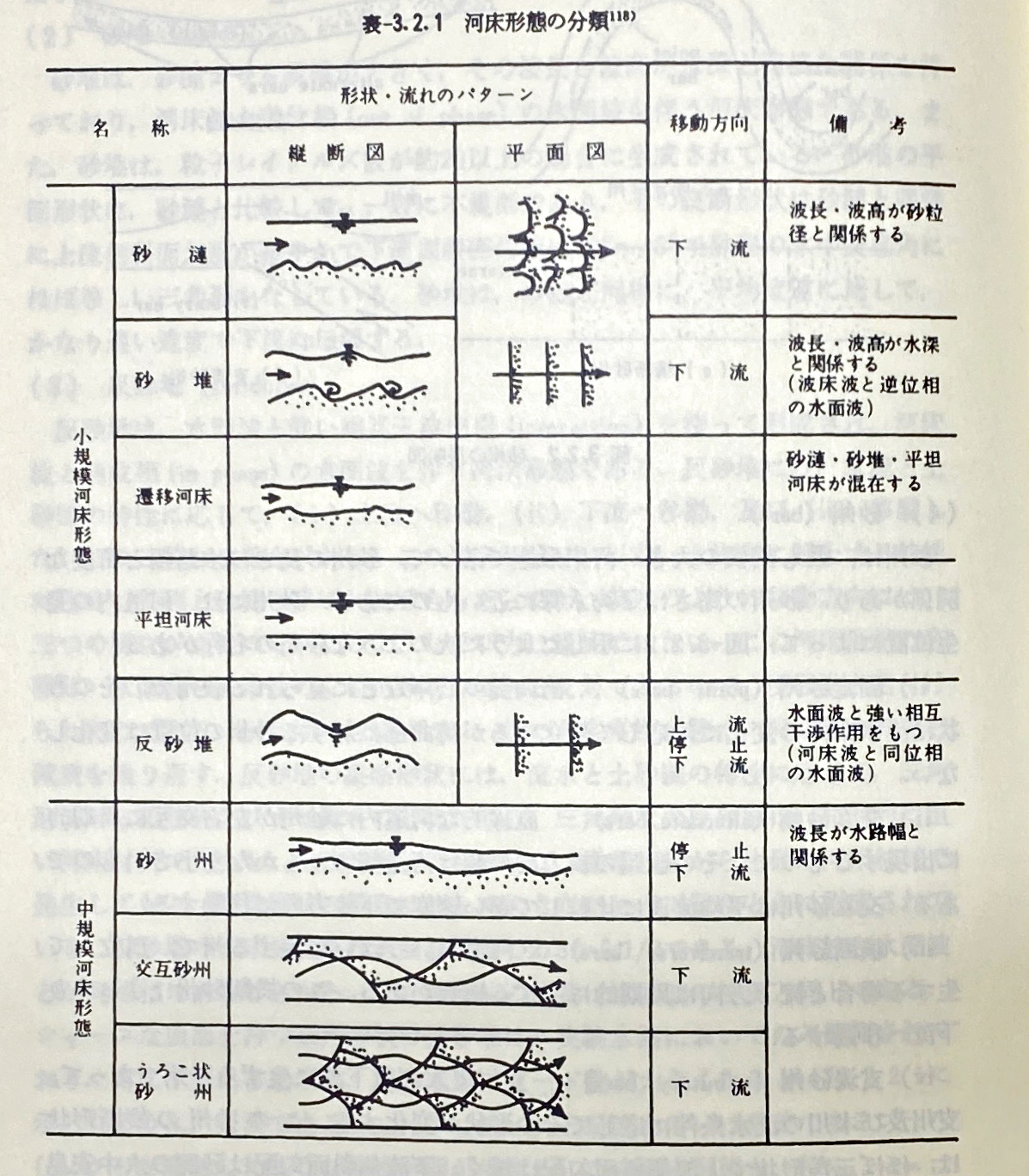
河床波(ここでは砂堆)上の流れを模式的に示すと下図のとおりである。⁷

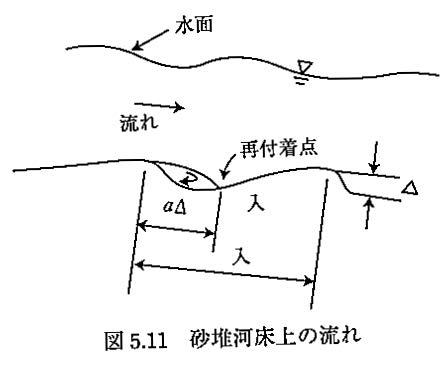
ここで、（水深平均）流れに対する河床が与える抵抗を考えると「摩擦抵抗」と「剥離に伴う形状抵抗」に分類できる。 Manningの公式のような平均流速公式ではこの両者の影響が混ざって含まれることになる。

「摩擦抵抗」は河床材料によって決定するため対数則によって評価する。一方、「剥離に伴う形状抵抗」は河床波の形状を考慮して急拡損失の考え方により評価する。ここで河床波の形状が問題となる。模型実験では二次元水路を使用することにより河床波の形状を計測することは比較的容易であるが、実河川では難しく、近年の研究で高解像度のセンサーを用いた実河川の河床波の計測事例が報告されている⁸が、まだ一般的とは言えず、実河川の河床波形状を計測すること難しい。

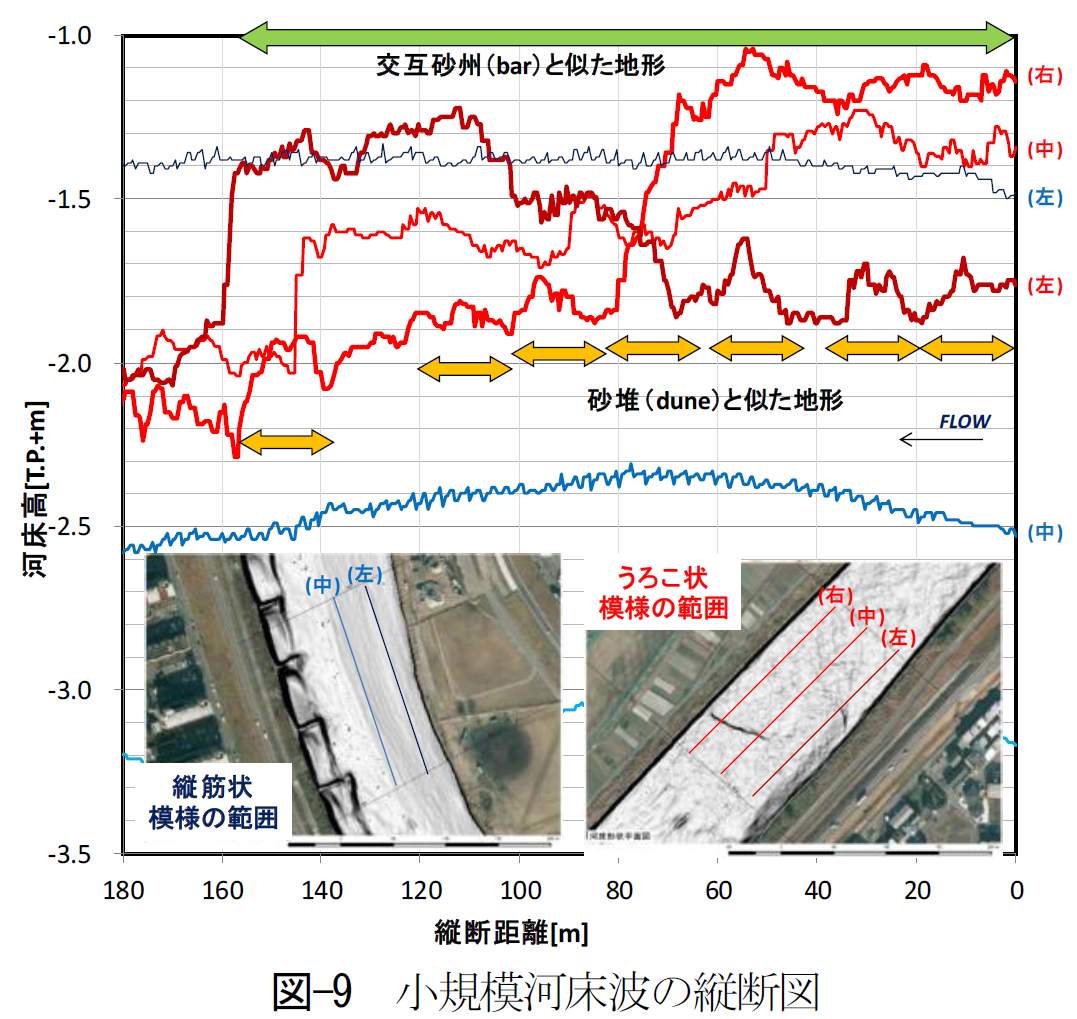
さらに、実河川の流れは非定常にであり、流れの規模によって河床波の形状が変化する。このような実河川における出水中の河床波の変化を計測事例はほとんど報告されておらず⁹,¹⁰、実態は不明である。

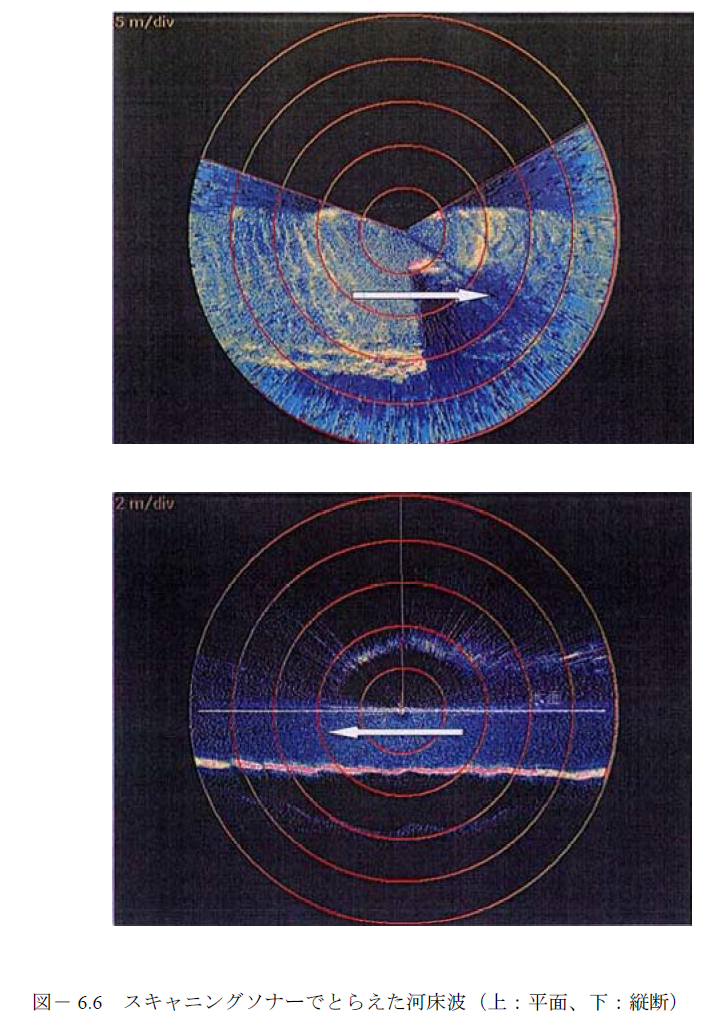
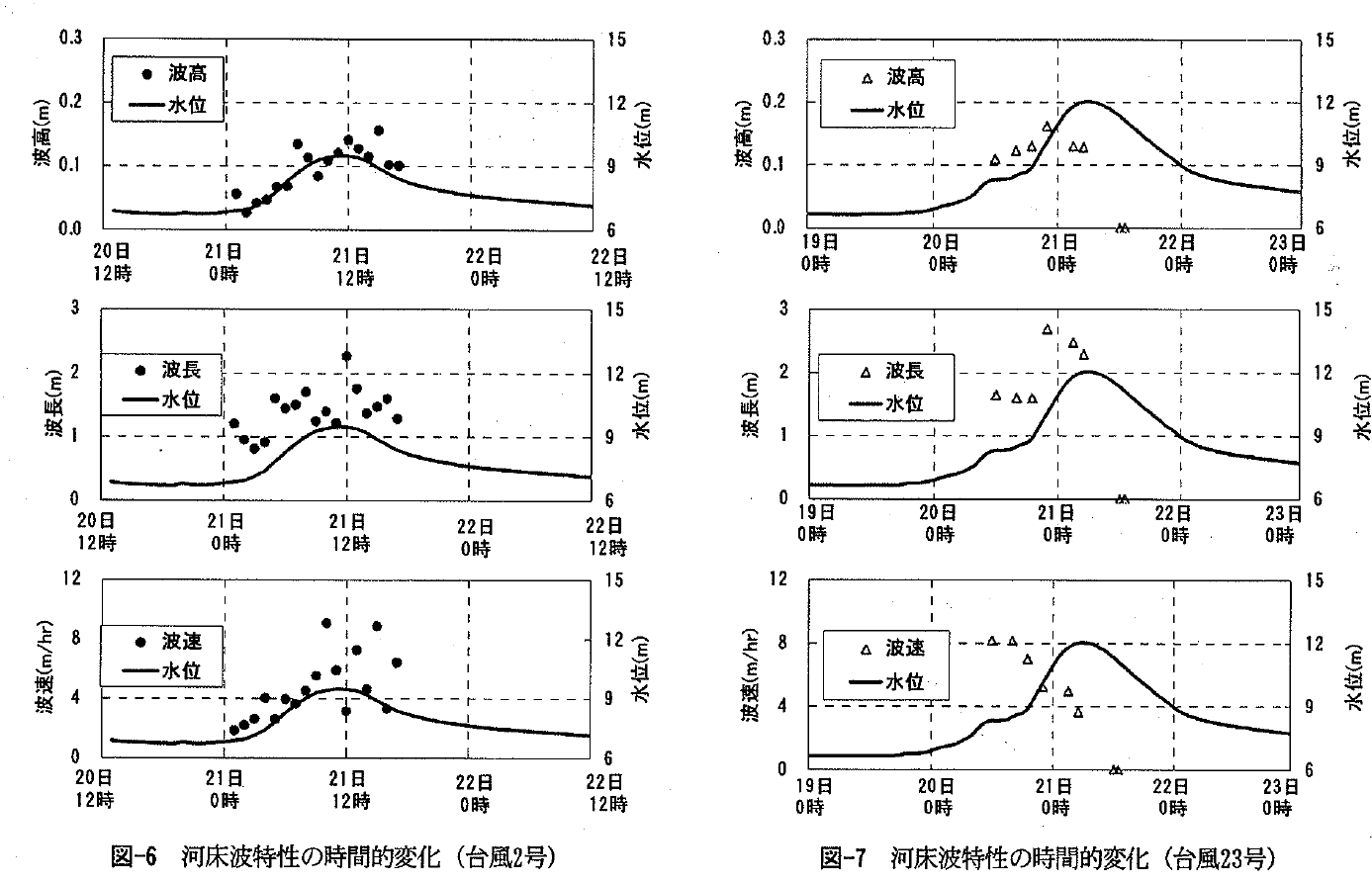
これらより実河川の河床抵抗を厳密に推定することは難しいことが理解できる。そのため、Manningの公式が積極的に代用されている。前項にはManningの粗度係数は水深によってほとんど変化しないと示したが、これは河床波形状が変化しない条件で成立し、変化する場合には形状抵抗による損失が変化するため、Manningの粗度係数も変化する。

なお、Manningの粗度係数は一定値として取り扱うことが一般的である。観測資料が十分でなく、大規模出水時に観測データから同定された値を使うためである。

河床波の変化を考慮した河床抵抗の評価方法

前項のとおり、実河川での検証が難しいため、模型実験結果を元に河床抵抗の評価を行う。

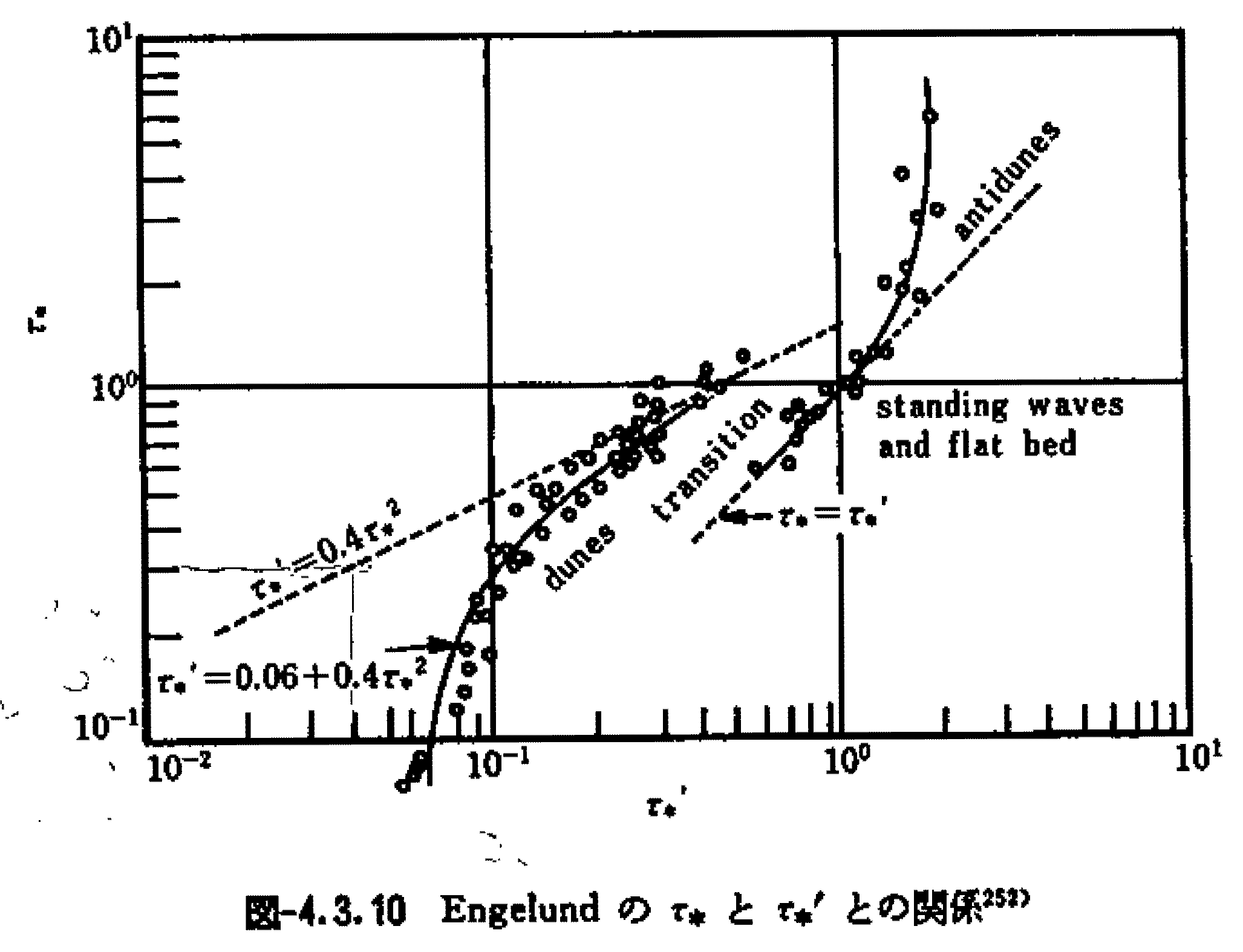
Engelund¹¹は河床抵抗を以下のようにモデル化した。

$\begin{align} \tau_* = \tau_*^{\prime} + \tau_*^{\prime\prime} \end{align}$

ここで、 $\tau_*$ :全無次元掃流力、 $\tau_*^{\prime}$ :摩擦抵抗による無次元掃流力（=無次元有効掃流力）、 $\tau_*^{\prime\prime}$ :形状抵抗による無次元掃流力である。

相似則より $\tau_*$ は $\tau_*^{\prime}$ のみの関数であることを示した。これより実験結果を使用して次図¹²の関係式を示した。

さらに、岸・黒木[^5]はEngelundの相似則を修正し、 $\tau_*$ は $\tau_*^{\prime}$ , $R/d$ の関数となることを示し、次図[^12]の関係を示した。

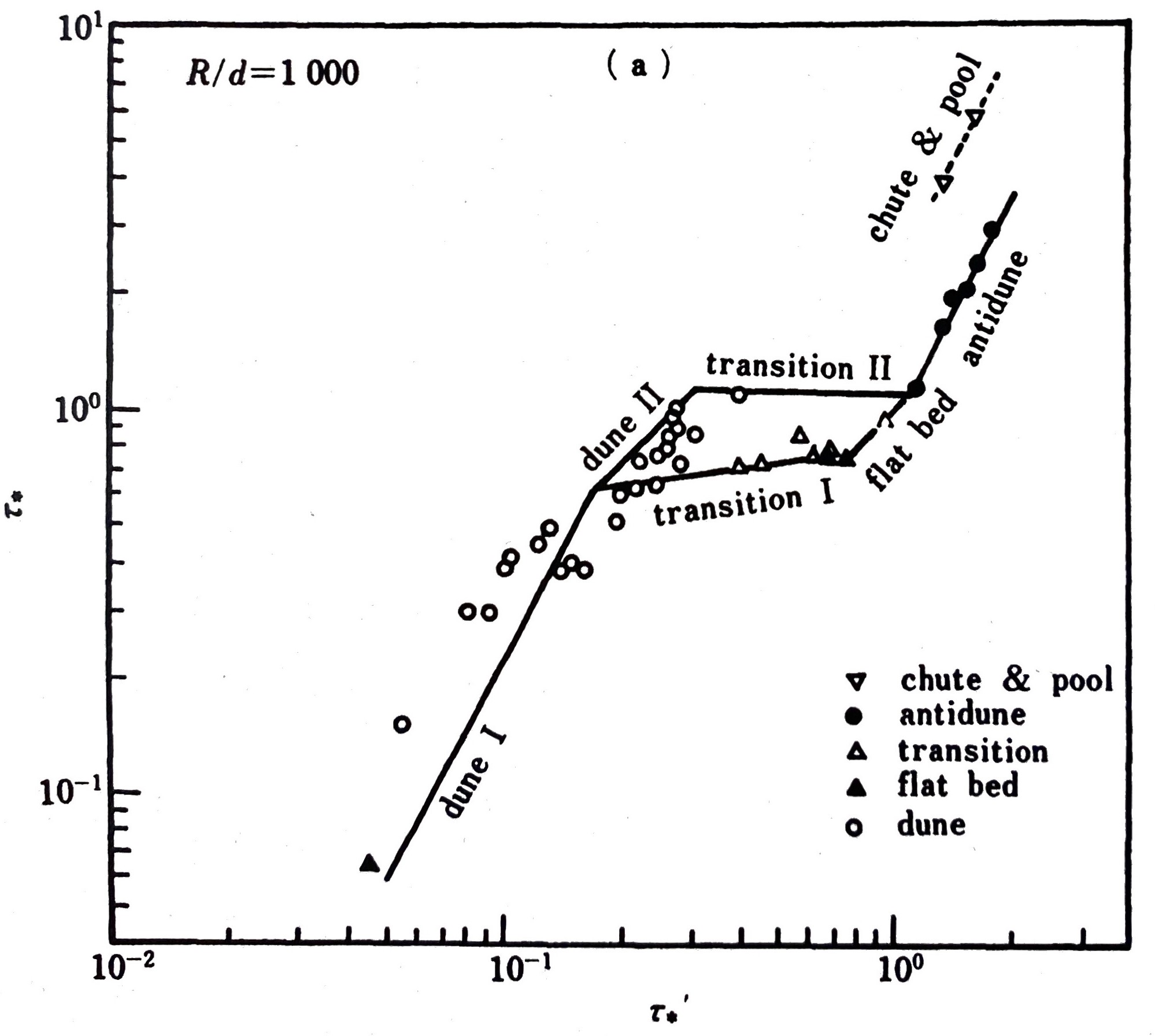
現時点ではこれが最も有用な研究成果と考えられる。

参考までにEngelundと岸・黒木の研究成果を比較する。両者による無次元掃流力-有効無次元掃流力の図を重ね合わせると次図のとおりである。なお、岸・黒木の図は $R/d$ が1000、500、100の3ケースを示す。

両者を比較するとdune領域、flat-bed・antidune領域ではそれほど大きな差異はないが、transition領域の取り扱いが異なっている。 Engelundはtransition領域の変化が不明なため定式化していないが、岸・黒木は定式化しており、この領域の取り扱いが $R/d$ によって異なっている。よって、transition領域の影響を考慮するためには岸・黒木の方法を使う他はない。

河床波の変化による流れ場への影響を理解しやすくするため、岸・黒木の図を $\phi$ と $\tau_*$ の関係に変換した図[^12]を以下に示す。

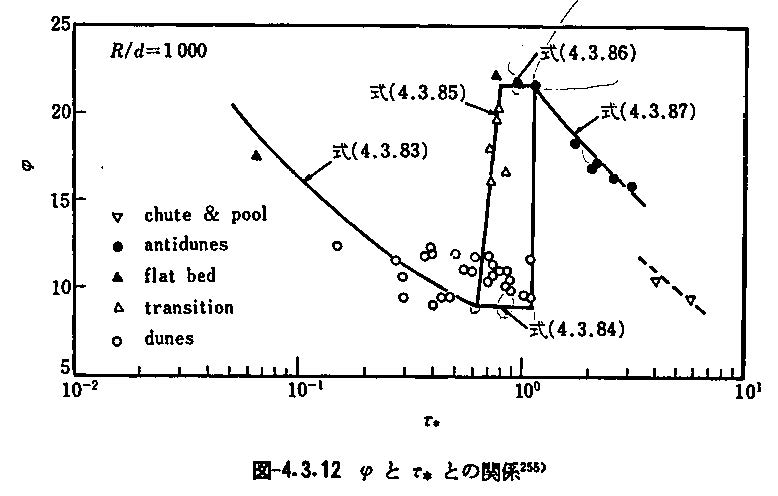
縦軸の $\phi=V/u_*$ は流れやすさを示すため、transition領域で急激に流れやすくなる、つまり、河床抵抗が減少することが理解できる。

岸・黒木の方法による河床抵抗の評価

岸・黒木の方法による河床抵抗の評価の計算方法について示す。次図（再記）の各領域区分の無次元掃流力 $\tau_*$ と有効無次元掃流力 $\tau_*^{\prime}$ の関係式は以下のとおりとなっている。

$\begin{align} \rm{dune1} : \tau_*^{\prime} &= 0.21\tau_*^{1/2} \\ \rm{dune2} : \tau_*^{\prime} &= 1.49(R/d)^{-1/4}\tau_* \\ \rm{flat\text{-}bed} : \tau_*^{\prime} &= \tau_* \\ \rm{antidune} : \tau_*^{\prime} &= 0.264(R/d)^{1/5}\tau_*^{1/2} \\ \rm{transition1} : \tau_*^{\prime} &= 6.5 \times 10^7(R/d)^{-5/2} \tau_*^{11/2} \end{align}$

また、dune領域とtransition領域、flat-bed領域とantidune領域の区分は次式となる。

$\begin{align} \rm{dune \text{ -- } transition} : \tau_* &= 0.02(R/d)^{1/2} \\ \rm{flat\text{-}bed \text{ -- } antidune} : \tau_* &= 0.07(R/d)^{2/5} \end{align}$

上図中のtransition2領域は関係式が設定されていない。transition2はdune2とantiduneを直線で繋いでおり、dune領域の上限値を示している。 transition領域では複雑な変化を示すため定式化は難しいが、岸・黒木の方法より、dune1 -- transition1 -- flat-bed -- antiduneの過程で遷移する(図中赤線)ものと考える。なお、antiduneは射流場のみで発生するため、ほとんど沖積河川の場合、flat-bedまでの変化を考慮すれば良い。

岸・黒木の方法の課題

河床波の遷移の履歴

ここまでに示した考え方は基本的に定常、等流、平衡を前提に構築されている。また、模型実験のデータを基に関数をフィッティングしている。

実河川の適用性は、Engelund[^11]はRio Grande川での観測データと一致することを示しており、岸・黒木[^5]も同じデータを用いて妥当性を示している。しかし、岸・黒木は石狩川の観測データとの比較により水理量と河床形状の関係が常に平衡にはならずに履歴の影響を受けること示しており、手法の適用上の課題を指摘している。

今後はより多くの河川で観測を実施して手法の適用性を検証する必要がある。

河床波の形状抵抗の直接評価

Engelundおよび岸・黒木の方法は、相似を仮定して無次元掃流力と有効無次元掃流力の関係を用いて河床波の影響を評価しているが、河床波の形状損失を直接評価する方が理想的である。

この方法は、これまでの研究では一次元流れを仮定した急拡損失による評価が行われてきたが、乱流モデルを用いた鉛直二次元または三次元解析によって評価する必要がある。また、現時点では実河川による検証データの取得が難しいため、模型実験を基本に検証を進めることが望ましい。

参考：流砂量評価における有効掃流力

掃流力は流れにとっては抵抗になるが河床土砂にとっては駆動力となる。その力は全抵抗から形状抵抗を差し引いた有効掃流力である。そのため、河床波の遷移は掃流砂量にも大きな影響を与える。

日本で最も使用される芦田・道上の掃流砂量式には有効掃流力が含まれている。これはdune上の流れを想定していることを意味しており、本来であれば、河床波形状に応じてこの式形を変更する必要がある。

また、使用頻度は低いが、佐藤・吉川・芦田の式（土研公式）ではManningの粗度係数によって式形を変更している。これは、河床波形状の影響を示しているが、河床波形状はManningの粗度係数のみでは決定しないため、使用の際には注意が必要である。

参考図書

リンク

Github

Jupyter Notebook Viewer

Chow,V.,T.: Open-channel hydraulics, pp.110-113, McGraw-Hill, 1959.↩
土木学会水理委員会水理公式集改訂小委員会 : 水理公式集, p.89, 土木学会, 1999.↩
建設省河川局,日本河川協会 : 建設省河川砂防技術基準(案)同解説調査編, p.133, 技報堂出版, 1997.↩
椿東一郎 : 水理学I, p.110, 森北出版, 1973.↩
水理委員会移動床流れの抵抗と河床形状研究小委員会 : 移動床流れにおける河床形態と粗度, 土木学会論文報告集第210号, pp.65-91, 1973.↩
Simons,D.B.,Şentürk, F. : Sediment Transport Technology, Water Resources Publications, 1977.↩
芦田和男,江頭進治,中川一 : 21世紀の河川学:安全で自然豊かな河川を目指して, p.121, 京都大学学術出版会, 2008.↩
例えば、秋田麗子,西口亮太,野間口芳希 : 水中の河床地形の面的計測とその活用方策について, 河川技術論文集, 第23巻, pp.173-178, 2017.↩
高部一彦，人見寿，坂野章，山本浩一 : 涸沼川における河床波観測及び解析, 河川技術論文集, 第11巻, pp.387-392, 2005.↩
末次忠司, 日下部隆昭, 坊野聡子 : 土砂管理施策のためのキーノート, 国土技術政策総合研究所資料, No.231, 2005.↩
Engelund F. : Hydraulic Resistance of Alluvial Streams, Journal of the Hydraulics Division, Vol. 92, Issue 2, pp.315-326, 1966. ↩
河村三郎 : 土砂水理学, pp.226-230, 森北出版, 1982.↩