趣味で計算流砂水理

趣味で計算流砂水理 Computational Sediment Hydraulics for Fun Learning

数値計算とか河川工学とかプログラミングのことを書いています

MENU

河川技術者向け基礎講座　準二次元不等流計算4/4：一般断面の不等流計算3-分割断面法+分割断面間の干渉を考慮（平均流速公式レベル3）

R

教科書の「不等流計算」は理解できるが、実務で汎用される「準二次元不等流計算」がなかなか理解し難い方に向けて、記事を書きました。 多分相当わかりやすいと思いますので、河川行政に関わる方やコンサルの方に読んで頂きたいです。

全4回の第4回目です。

本記事はGitHub、nbviewer、Colab、Marp（スライド形式）でも公開しています。

※Colabの解説記事はこちら

※Marpの解説記事はこちら

a nbviewer Open In Colab a

はじめに

  • 前回説明した分割断面法（平均流速公式レベル2）では、分割断面間で流れの干渉は生じないこと条件とした。
  • 今回説明する平均流速公式レベル3(以降、本手法)は、分割断面間での流れの干渉による運動量損失を考慮したモデルとなる。
  • 流れ同士の干渉による損失と樹木群と流れの干渉による損失を考慮する。
  • 種々の研究成果があるが、河道計画で広く使用されている福岡・藤田:複断面河道の抵抗予測と河道計画への応用の考え方を基本に説明を行なう。

A

  • おさらい
    • 分割断面ごとに変わる：流速、河積、潤辺、粗度係数など
    • 分割断面ごとに変わらない：水位、エネルギー勾配

分割断面間の干渉とは？

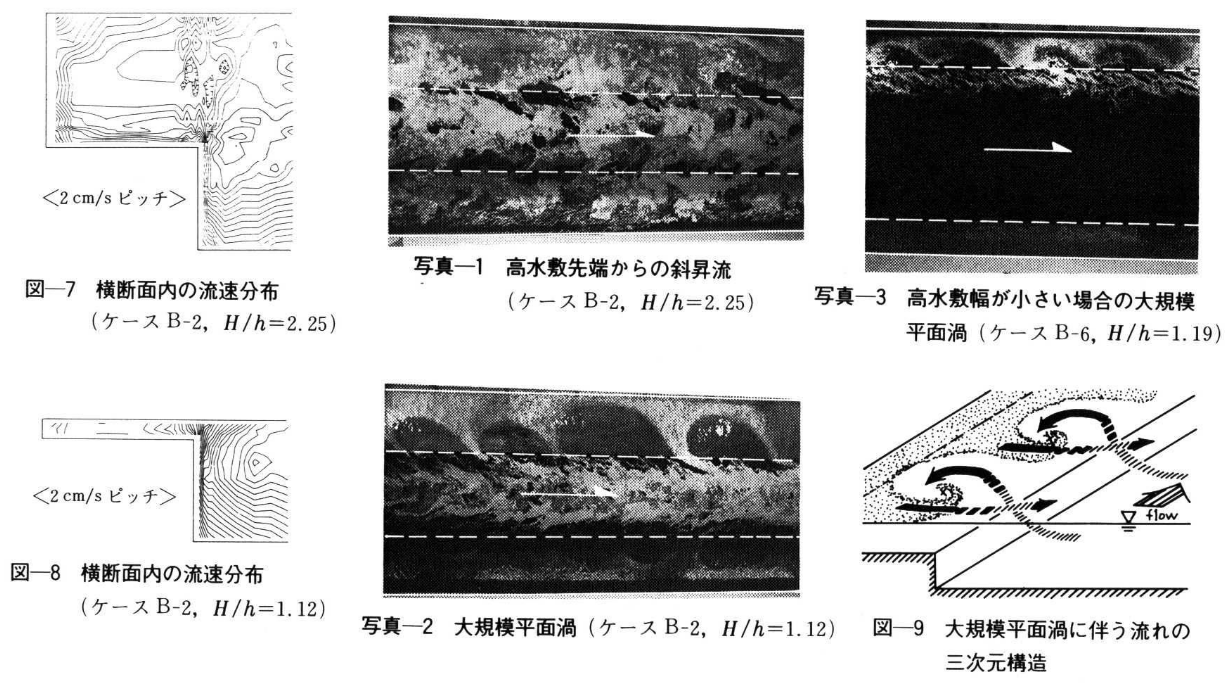
  • 低水路・高水敷間など各領域の流速差が大きい場合、境界付近には水平渦が発生することが知られている。
  • 本手法では、この渦による運動量損失が水位に影響を及ぼすと考えている。

石川ら,2011:洪水航空写真に捉えられた低水路河岸渦の特性に関する比較研究 A A

  • 前回講義でも少し説明したが、横断面内の流速分布は、高水敷・低水路間で不連続的となり、渦の影響を受けていることは明らかである。
  • 実河川スケールでの観測データが少なく、その影響度合いは不明な点が多い。

福岡,藤田,1989:複断面河道の抵抗予測と河道計画への応用

A

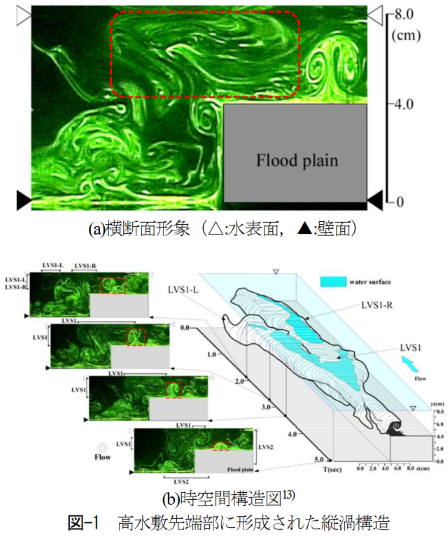
補足：斜昇流の存在

  • 高水敷の流速が大きい場合、斜昇流と呼ばれる低水路から高水敷に向かう流れ(縦渦)が存在することが知られている。
  • 今回説明する干渉の影響では、斜昇流による損失は考慮されていない。
  • 観測、解析技術の進展により、徐々に実態が解明されつつある。実河川での観測例は無い（多分）。

渡辺ら2022:高水敷先端部の吸込み操作に伴う複断面開水路流れの変化特性

A

基礎式

運動方程式（流下方向）

本手法による不等流計算の運動方程式は次式を用いる。

\begin{align} & \dfrac{d}{dx}\left( \frac{\beta Q^2}{2gA^2} + H \right) = -\dfrac{T}{\rho g A} \end{align}

ここに、Q:流量、H：水位、A=\sum A_n：河積、T：横断面全体の作用するせん断力、\beta：運動量補正係数とする。

前回の分割断面法のときと同様である。 今回は、右辺の生成項を変更を加える。

これまでは、生成項は河床の摩擦損失のみを考慮したが、本手法では、分割断面間の流れ同士の干渉による損失および樹木群と流れの干渉による損失を追加する。

これらを計算するためには各分割断面の流速が必要となる。次項に計算方法を示す。

横断方向の流速分布

各分割断面で流下方向に等流が成立すると仮定すると、 各分割断面で次式が成り立つ。

\begin{align} \dfrac{ T_n}{\rho g } = I A_n \end{align}

ここで、 分割断面間の流れ同士の干渉によるせん断力\tau^{\prime} (横断面の単位長さあたり)は次式で示す。

\begin{align} \tau^{\prime} & = \rho f^{\prime} \Delta u |\Delta u | \end{align}

また、 樹木群と流れの干渉によるせん断力\tau(横断面の単位長さあたり)は次式で示す。

\begin{align} \tau & = \rho f u^2 \end{align}

ここに、\Delta uは境界面を介して隣り合う分割断面間での断面平均流速差、f,f^{\prime}は流れ間、流れと樹木間の境界混合係数とする。

河床摩擦損失はマニング則を用いて次式とする。

\begin{align} I A_n = \dfrac{ {n}^2 {u}^2}{ {R}^{1/3} } {S} \end{align}

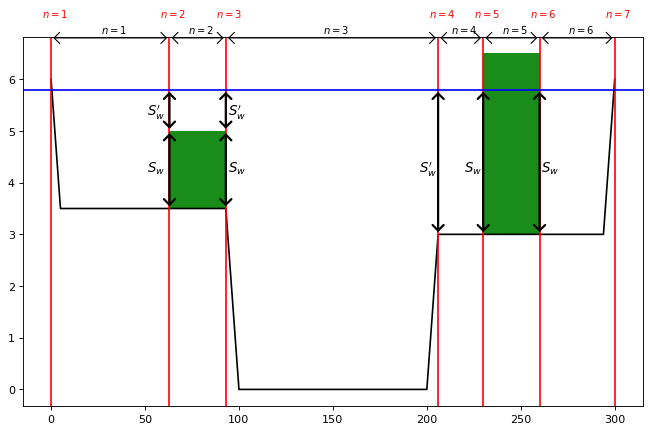
具体例として、次の断面のうち、n=3と2の分割断面について運動方程式を立ててみる。

A

分割断面n=3の運動方程式

\begin{align} \dfrac{ {n_n}^2 {u_n}^2}{ {R_n}^{1/3} } {S_n} +\dfrac{ \tau_n {S_w}_n}{\rho g} + \dfrac{ \tau^{\prime}_n {S^{\prime}_w}_n + \tau^{\prime}_{n+1} {S^{\prime}_w}_{n+1} }{\rho g} & = A_n I \\ \tau_n &= \rho f_n u_n^2 \\ \tau^{\prime}_n &= \rho f^{\prime}_n \Delta u |\Delta u | = \rho f^{\prime}_n (u_n-u_{n-1}) |u_n-u_{n-1}| \\ \tau^{\prime}_{n+1} &= \rho f^{\prime}_{n+1} \Delta u |\Delta u | = \rho f^{\prime}_{n+1} (u_n-u_{n+1}) |u_n-u_{n+1}| \end{align}

A

分割断面n=2の運動方程式

\begin{align} \dfrac{ {n_n}^2 {u_n}^2}{ {R_n}^{1/3} } {S_n} + \dfrac{ \tau^{\prime}_n {S^{\prime}_w}_n + \tau^{\prime}_{n+1} {S^{\prime}_w}_{n+1} }{\rho g} & = A_n I \\ \tau^{\prime}_n &= \rho f^{\prime}_n \Delta u |\Delta u | = \rho f^{\prime}_n (u_n-u_{n-1}) |u_n-u_{n-1}| \\ \tau^{\prime}_{n+1} &= \rho f^{\prime}_{n+1} \Delta u |\Delta u | = \rho f^{\prime}_{n+1} (u_n-u_{n+1}) |u_n-u_{n+1}| \end{align}

A

すべての分割断面に対応できるように、一般化すると次式となる。

\begin{align} \dfrac{ {n_n}^2 {u_n}^2}{ {R_n}^{1/3} } {S_n} +\dfrac{ \tau_n {S_w}_n + \tau_{n+1} {S_w}_{n+1}}{\rho g} + \dfrac{ \tau^{\prime}_n {S^{\prime}_w}_n + \tau^{\prime}_{n+1} {S^{\prime}_w}_{n+1} }{\rho g} & = A_n I \\ \tau_n &= \rho f_n u_n^2 \\ \tau_{n+1} &= \rho f_{n+1} u_n^2 \\ \tau^{\prime}_n &= \rho f^{\prime}_n \Delta u |\Delta u | = \rho f^{\prime}_n (u_n-u_{n-1}) |u_n-u_{n-1}| \\ \tau^{\prime}_{n+1} &= \rho f^{\prime}_{n+1} \Delta u |\Delta u | = \rho f^{\prime}_{n+1} (u_n-u_{n+1}) |u_n-u_{n+1}| \end{align}

よって、分割断面の数だけ方程式が成立する。 なお、分割断面n=5は流速0のため、これを除いた5分割断面の計算を行なう。

さらに、以下の連続式を連立させることにより、各分割断面の流速と損失勾配Iを同時に解くことができる。

\begin{align} Q = \displaystyle \sum^n {u_n}A_n \end{align}

ここで得られた流速から求めるせん断力を流下方向の運動方程式に代入することにより縦断水位を計算する。 なお、流水間のせん断力は前述のとおり分割断面間でキャンセルされるため、計算しないことに留意する。

\begin{align} \dfrac{T}{\rho g A} = \dfrac{1}{A}\left( \sum_n^{nmax} \left( \dfrac{ {n_n}^2 {u_n}^2}{ {R_n}^{1/3} } {S_n} \right) + \sum_n^{nmax+1} \left( \dfrac{ \tau_n {S_w}_n}{\rho g} \right) \right) \end{align}

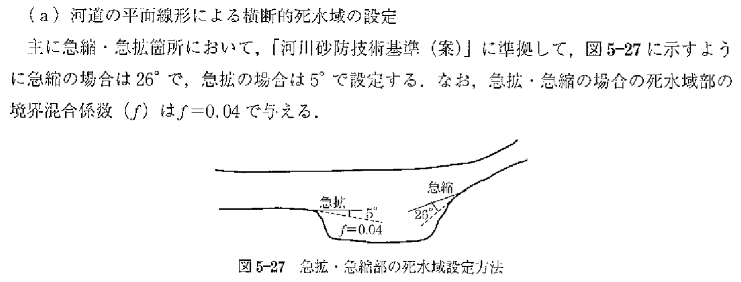
さらに、以下のように有効断面の外側に死水域を設定する場合は下式のように境界部分のせん断力を考慮する。

\begin{align} \dfrac{T}{\rho g A} = \dfrac{1}{A}\left( \sum_n^{nmax} \left( \dfrac{ {n_n}^2 {u_n}^2}{ {R_n}^{1/3} } {S_n} \right) + \sum_n^{nmax+1} \left( \dfrac{ \tau_n {S_w}_n}{\rho g} \right) + \dfrac{\tau^{\prime}_0 {S^{\prime}_w}_0}{\rho g} + \dfrac{\tau^{\prime}_{nmax+1} {S^{\prime}_w}_{nmax+1}}{\rho g} \right) \end{align}

河道計画検討の手引き

A

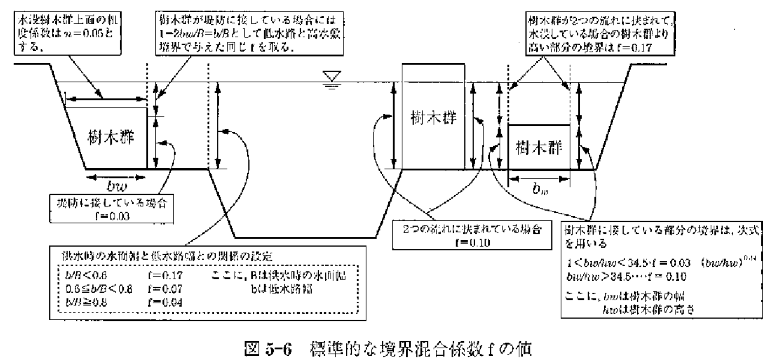
境界混合係数について

境界混合係数の標準値は以下のように定義されている。

私の感覚では厳密にこの図に則って計算している事例は少ないように思う。 高水敷・低水路間だけしっかり決めてあげれば良い気がする。

河道計画検討の手引き

A

限界水深、等流水深の定義

一般断面の基礎式を用いて、限界水深、等流水深を矩形断面と同様に定義で設定することは難しいため、便宜的に以下のとおりに設定する。

等流水深

全ての損失による水頭の勾配が河床勾配i_bと釣り合う状態を等流と定義してその水深を等流水深とする。 なお、一般断面では水深を用いないため、正確には等流時の水位となる。

\begin{align} \dfrac{T}{\rho g A} = i_b \end{align}

となり、これを満足する水位Hを反復法などにより求めれば良い。

限界水深

フルード数が1となる水位を限界流時の水位とする。

フルード数はエネルギー保存則の分母が0より、

\begin{align} 1 &= \dfrac{\alpha q^2}{gh^3} \\ Fr&= \dfrac{V}{ \sqrt{\dfrac{gh}{\alpha}}} \\ Fr&= \dfrac{Q}{A\sqrt{\dfrac{gh}{\alpha}} } \end{align}

となるが、平方根の中に水深hが含まれるため、一般断面ではそのままでは計算できない。

そのため、分割断面法では水深hの代替として井田の合成径深R_cを使用することが多い。その他には径深R=A/S、A/Bを用いることもある。

参考：FORUM8ソフトウェア：等流・不等流の計算・3DCAD Ver.9 Q&A

離散化

横断方向流速分布の式は以下となり、分割断面数分の式が成り立つ。

\begin{align} \dfrac{ {n_n}^2 {u_n}^2}{ {R_n}^{1/3} } {S_n} +\dfrac{ \tau_n {S_w}_n + \tau_{n+1} {S_w}_{n+1}}{\rho g} + \dfrac{ \tau^{\prime}_n {S^{\prime}_w}_n + \tau^{\prime}_{n+1} {S^{\prime}_w}_{n+1} }{\rho g} & = A_n I \\ \tau_n &= \rho f_n u_n^2 \\ \tau_{n+1} &= \rho f_{n+1} u_n^2 \\ \tau^{\prime}_n &= \rho f^{\prime}_n \Delta u |\Delta u | = \rho f^{\prime}_n (u_n-u_{n-1}) |u_n-u_{n-1}| \\ \tau^{\prime}_{n+1} &= \rho f^{\prime}_{n+1} \Delta u |\Delta u | = \rho f^{\prime}_{n+1} (u_n-u_{n+1}) |u_n-u_{n+1}| \end{align}

以下の連続式を連立させることにより、各分割断面の流速と損失勾配Iを求める。

\begin{align} Q = \displaystyle \sum^n {u_n}A_n \end{align}

縦断水位の離散化はこれまでと同様に次式となる。 なお、i:上流側、i-1:下流側とする。

\begin{align} \left(\frac{\beta_i Q^2}{2gA^2_i} + H_i \right) -\left( \frac{\beta_{i-1} Q^2}{2gA_{i-1}^2} + H_{i-1} \right) &= \dfrac{1}{2}\left(\dfrac{T_i}{\rho g A_i} + \dfrac{T_{i-1}}{\rho g A_{i-1}} \right)\Delta x \\ A&=\sum A_n \end{align}

常流の場合、下流から逐次計算を行なうため未知数はH_iのみとなる。

数値計算方法

縦断水位はこれまで同様のため説明を省略し、横断方向流速分布の計算方法をのみを示す。この計算にはかなり高度な数値計算手法が必要なため、理解できなくても問題ない。

計算するための前知識として以下の2手法を紹介する。

手法1：高次のニュートン法

高次のニュートン法は、通常のニュートン法と同様に以下のように示される。 なお、ボールド体は行列を示す。

\begin{align} \boldsymbol{X}^{n+1}&=\boldsymbol{X}^{n} -\frac{\partial \boldsymbol{f}(\boldsymbol{X}^n)}{\partial\boldsymbol{X}}^{-1}\boldsymbol{f}(\boldsymbol{X}^n) \end{align}

上式の右辺第二項を\boldsymbol{r}とおく。

\begin{align} \boldsymbol{r}&=\frac{\partial \boldsymbol{f}(\boldsymbol{X}^n)}{\partial \boldsymbol{ X}}^{-1}\boldsymbol{f}(\boldsymbol{ X}^n) \end{align}

\boldsymbol{r}は\dfrac{\partial \boldsymbol{f}( \boldsymbol{X}^n)}{\partial \boldsymbol{X}}の逆行列が計算できれば、容易に求めることができる。

よって、下式で解の更新を行なう。

\begin{align} \boldsymbol{X}^{n+1}&=\boldsymbol{X}^{n}-\boldsymbol{r} \end{align}

手法2：TDMA法

TDMA法（トーマス法）とは係数行列が三重対角行列の連立一次元方程式の効率的な数値解法である。 ガウスの消去法(直接法)の計算量は分割数Nの3乗であるが、TDMA法はNの数倍程度の計算量となる。

導出はwikipediaを参照ください。https://en.wikipedia.org/wiki/Tridiagonal_matrix_algorithm

def TDMA(a,b,c,d):
    x, P, Q = np.empty_like(a), np.empty_like(a), np.empty_like(a)
    n = len(x)
    
    P[0], Q[0] = -c[0]/b[0], d[0]/b[0]
    for i in range(1, n):
        P[i] = -  c[i]                /(a[i]*P[i-1] + b[i])
        Q[i] =  (-a[i]*Q[i-1] + d[i])/(a[i]*P[i-1] + b[i])
        
    x[-1] = Q[-1]
    for i in range(n-2, -1, -1):
        x[i] = P[i]*x[i+1] + Q[i]
        
    return x
  • 大規模演算に使用することを意識するとメモリ節約版も知っておくと良い。引数をそのまま使うため、参照渡しの場合、引数の値が変わることに注意

参考： https://nekodamashi-math.blog.ss-blog.jp/2017-12-03-2

def lmTDMA(a,b,c,d):
    n = len(a)
    #! 前進消去
    for i in range(1, n):
        ratio=a[i]/b[i-1]
        b[i]=b[i] - ratio*c[i-1]
        d[i]=d[i] - ratio*d[i-1]

    #! 後退代入
    d[-1]=d[-1]/b[-1]
    for i in range(n-2, -1, -1):
        d[i]=(d[i]-c[i]*d[i+1])/b[i]

    return d

計算方法

分割断面の運動方程式をuについて展開する。

\begin{align} \dfrac{ {n_n}^2 {u_n}^2}{ {R_n}^{1/3} } {S_n} +\dfrac{ \tau_n {S_w}_n + \tau_{n+1} {S_w}_{n+1}}{\rho g} + \dfrac{ \tau^{\prime}_n {S^{\prime}_w}_n + \tau^{\prime}_{n+1} {S^{\prime}_w}_{n+1} }{\rho g} & = A_n I \\ \tau_n &= \rho f_n u_n^2 \\ \tau_{n+1} &= \rho f_{n+1} u_n^2 \\ \tau^{\prime}_n &= \rho f^{\prime}_n \Delta u |\Delta u | = \rho f^{\prime}_n (u_n-u_{n-1}) |u_n-u_{n-1}| \\ \tau^{\prime}_{n+1} &= \rho f^{\prime}_{n+1} \Delta u |\Delta u | = \rho f^{\prime}_{n+1} (u_n-u_{n+1}) |u_n-u_{n+1}| \end{align}

以下のとおりに式変形できる。

\begin{align} a_n X_{n-1}+b_n X_{n}+c_n X_{n+1}-A_n=0 \end{align}

ここに、

\begin{align} X_n&=\dfrac{u_n}{\sqrt{I}} \\ a_n&=-\frac{\rho {f^{\prime}}_{n} {S^{\prime}_w}_{n}(X_{n}-X_{n-1}) \sigma_1} {\rho g}\\ b_n&=\left\lbrace \frac{ {n_n}^2 }{ {R_n}^{1/3} } {S}_n +\frac{ \rho {f}_{n} {S_w}_{n}+\rho {f}_{n+1} {S_w}_{n+1}}{\rho g}\right\rbrace X_n - a_n - c_n \\ c_n&=-\frac{\rho {f^{\prime}}_{n+1} {S^{\prime}_w}_{n+1}(X_{n}-X_{n+1}) \sigma_2} {\rho g}\\ \sigma_1 & = \dfrac{(u_n-u_{n-1})}{|u_n-u_{n-1}|} \\ \sigma_2 & = \dfrac{(u_n-u_{n+1})}{|u_n-u_{n+1}|} \end{align}

全分割断面の方程式をベクトル形式で記述すると以下となる。なお、分割断面5は、水深が0となるため、省いて行列を構成する。

\begin{align} \boldsymbol{X}=\dfrac{1}{\sqrt{I}} \begin{pmatrix} u_1 \\ u_2 \\ u_3 \\ u_4 \\ u_6 \\ \end{pmatrix} \end{align}
\begin{align} \boldsymbol{\alpha(\boldsymbol{X})}= \begin{pmatrix} b_1 && c_1 && 0 && 0 && 0 \\ a_2 && b_2 && c_2 && 0 && 0 \\ 0 && a_3 && b_3 && c_3 && 0 \\ 0 && 0 && a_4 && b_4 && c_4 \\ 0 && 0 && 0 && a_6 && b_6 \\ \end{pmatrix} \end{align}
\begin{align} \boldsymbol{\beta}= \begin{pmatrix} A_1 \\ A_2 \\ A_3 \\ A_4 \\ A_6 \\ \end{pmatrix} \end{align}
\begin{align} \boldsymbol{f}(\boldsymbol{X})= \boldsymbol{\alpha(\boldsymbol{X})}\boldsymbol{X} - \boldsymbol{\beta} \end{align}

\boldsymbol{\alpha}はXの関数のため、直接計算することができない。

そのため、高次のニュートン法を用いて反復計算を行なう。 \boldsymbol{f}の微分式は以下となる。

\begin{align} \frac{\partial \boldsymbol{f}(\boldsymbol{X})}{\partial \boldsymbol{X}}= \begin{pmatrix} 2b_1 && 2c_1 && 0 && 0 && 0 \\ 2a_2 && 2b_2 && 2c_2 && 0 && 0 \\ 0 && 2a_3 && 2b_3 && 2c_3 && 0 \\ 0 && 0 && 2a_4 && 2b_4 && 2c_4 \\ 0 && 0 && 0 && 2a_6 && 2b_6 \\ \end{pmatrix} \end{align}

なお、上式は三重対角行列となるため、TDMAにより容易に逆行列が計算可能である。

ニュートン法による計算結果の\boldsymbol{X}と以下の連続式を連立させる。

\begin{align} Q = \displaystyle \sum^n {u_n}A_n \end{align}

よって、以下の式により\sqrt{I}, u_jを求める。

\begin{align} \sqrt{I}&=\frac{Q}{ \displaystyle \sum_n (X_n A_n)} \\ u_n&=\sqrt{I}\cdot X_n \end{align}

本手法の課題

  • 境界混合係数が大きすぎる
    • 境界混合係数は高水敷、低水路の区分が明確な大河川での水平渦を想定して設定された値である。そのため、適用範囲は限定的。
    • それにも関わらず、直轄河川では汎用されており、過大評価と考えられる。
  • 樹木群の死水域設定
    • 洪水流をみればわかるが、完全に死水域となる樹木群はほとんどない。
    • 実務では樹木群を死水域として取り扱うことが慣習化されており、過大評価と言える。

上記からわかるとおり、本手法では水位が高めに計算されがちである。

本手法の必要性、導入された経緯

  • 福岡、藤田、山本などによると、
    • 当時は痕跡水位から粗度係数を逆算することが行われており、様々な抵抗が粗度係数に含まれていた。
    • マニング則は、河床の摩擦抵抗を示した式であり、それ以外の抵抗は当然評価できない。
    • このような現象に基づかない計画は見直したい。つまり、流れの抵抗を適切に評価する必要がある。
  • 福岡、藤田は、流れの干渉、流れと樹木群の干渉に着目し、本手法を提案した。
  • 余談ですが、山本は低水路の粗度係数に着目し、流況と河床波の関係から粗度係数を評価する方法提案した。つまり、粗度係数は物理定数であることを改めて示した。
    • 河道計画検討の手引から、低水路の粗度係数の設定に重点を置いていることが理解できる。
    • 基本的には、推定粗度（流況によって決まる粗度）を使うことになっている。(未経験の出水に対して合理的に粗度係数を決める)
    • これらの知見は、半理論式と現地観測（涸沼川での河床波計測など）から見出されたが外挿も多く、不明な点が多い。

本手法には多くの問題点あるが、より正確に水位を計算したいという考えは正しいと思われる。

まとめ

本手法：平均流速レベル3による一次元（準二次元）不等流計算方法について説明を行った。

  • 直轄河川の流下能力評価を行なう方は、本手法の概要くらいは理解して欲しい。
  • 数値計算方法はかなり難しいので理解できなくても問題ない。
  • 複断面河道の水理は、かつて世界的に様々な研究がなされたため、興味のある方は参照すると面白い。
  • 複断面河道の詳細な流況はまだまだ不明な点も多く、近年でも特に実験に関する研究成果が見られる。

断面特性を計算するプログラム例

ボリュームがあるため、別ページに作成

a nbviewer Open In Colab

不等流計算のプログラム例

Coming soon.

参考文献

関連記事

computational-sediment-hyd.hatenablog.jp

備忘録：河川屋にはお馴染みの「特殊基準面」まとめ

R

一般に，標高の基準は東京湾平均海面T.P.+0mが使用されますが，我々の業界では，しばしば「特殊基準面」を用います． 「特殊基準面」とは，河川、水系等で定められた固有の基準面を示します。

代表的なものとして下表が挙げられます．

特殊基準面 東京湾平均海面（T.P.）への変換式 主に使用する河川
T.P. Tokyo Peil 東京湾平均海面 - 下記以外
K.P. Kitakami Peil 北上川基準水面 [T.P.] = [K.P.] - 0.8745 北上川
S.P. Shiogama Peil 塩釜港平均海面 [T.P.] = [S.P.] - 0.0873 鳴瀬川
Y.P. Yedogawa Peil 江戸川工事基準面 [T.P.] = [Y.P.] - 0.8402 利根川
A.P. Arakawa Peil 霊岸島量水標の最低潮位 [T.P.] = [A.P.] - 1.1344 荒川・中川・多摩川
O.P. Osaka Peil 大阪湾最低潮位 [T.P.] = [O.P.] - 1.3 淀川
A.P. Awa Peil 阿波量水標零点高 [T.P.] = [A.P.] - 0.8333 吉野川
T.P.w. ？ 四万十川（渡川）量水標零点高 [T.P.] = [T.P.w] + 0.113 渡川
B.S.L. Biwako basic Surface Level 鳥居川水位観測所の零点高 [T.P.] = [B.S.L.] + 84.371 琵琶湖

この「特殊基準面」は，正式な測量 でも使用することができます．

出典：河川砂防技術基準(案) 調査編 平成9年版 第21章 測量 - 第8節 水準基標測量

基準面はすべて東京湾平均海面T.P.+0mで良いとも思いますが，基準面の標高は地震ですぐに変わってしまうので，「特殊基準面」の使い勝手が良いこともあります．

令和６年能登半島地震の例 www.gsi.go.jp

比較のため，いくつかの「特殊基準面」を並べると以下のとおりです．

ソースコードはこちら

参考サイト： グラフをxkcd風に作成する #Python - Qiita

参考サイト

htmlの表作成は，tablesgeneratorhttps://www.tablesgenerator.com/を使用．

修正版：Pythonで写真からExif情報を抽出する

R

本記事のソースコードはGistでも公開しています．

gist9edf8ff48c8a64351994141b51d0bb9d

導入

news.mynavi.jp

基本的に上記サイトのままですが， Pillow==7.2.0以降では仕様変更に伴い，元のままだと動かないので一部修正しました．

  • 仕様変更:公式

7.2.0 - Pillow (PIL Fork) 10.3.0 documentation

  • 仕様変更:参考サイト

PillowでExif情報を遊ぶ ～辞書の復習を兼ねて～ #Python - Qiita

修正したプログラム

修正したプログラムは以下のとおりです．

"GPSLatitude"タグ，"GPSLongitude"タグの表記が変わったので，それに対応するように修正しました．

from PIL import Image
import PIL.ExifTags as ExifTags

def get_gps(fname):
    im = Image.open(fname)
    # EXIF情報を辞書型で得る
    exif = {
        ExifTags.TAGS[k]: v
        for k, v in im._getexif().items()
        if k in ExifTags.TAGS
    }
    # GPS情報を得る --- (*2)
    gps_tags = exif["GPSInfo"]
    gps = {
        ExifTags.GPSTAGS.get(t, t): gps_tags[t]
        for t in gps_tags
    }
    
    # 変更箇所
    conv_deg = lambda v : v[0] + (v[1] / 60.0) + (v[2] / 3600.0)
    
    lat = conv_deg(gps["GPSLatitude"])
    lat_ref = gps["GPSLatitudeRef"]
    if lat_ref != "N": lat = 0 - lat
    lon = conv_deg(gps["GPSLongitude"])
    lon_ref = gps["GPSLongitudeRef"]
    if lon_ref != "E": lon = 0 - lon
        
    return lat, lon

fname = 'XX.JPG'
get_gps(fname)

# (36.62291111111111, 138.24255277777777)

応用編：フォルダ内の全JPGファイルのEXIF情報を取得し，geojson形式で出力

作成した関数を用いて，フォルダ内の全JPGファイルのEXIF情報を取得して，位置情報をgeojson形式で出力するプログラムを作成しました．

import os
import glob
import pandas as pd
import geopandas as gpd
import numpy as np


#  ファイルリストを取得
path = r'C:\\Users'
fnames = glob.glob(path + '\\*.JPG')

# 位置情報を取得し，GeoDataFrameに格納
coords = [get_gps(f) for f in fnames]
c = np.array(coords)

df = pd.DataFrame({
'lat':c[:,0] ,'lon':c[:,1]
,'filename':[os.path.basename(f) for f in fnames]
,'fullpath': fnames
})

geometry = gpd.points_from_xy(df.lon, df.lat, crs="EPSG:4326")
gdf = gpd.GeoDataFrame(df, geometry=geometry)

# geojson形式で出力
out = gdf.to_file('photo.geojson', driver='GeoJSON')
del out

おまけ：QGISに写真付きで表示する

上記で作成したphoto.geojsonをQGISに読み込み，以下の手順を実施する．

  1. [シンボロジ] タブを開き，[単一定義]を選択し， [シンボルレイヤタイプ] を [ラスタ画像マーカー]にする．
  2. 図★箇所をクリックして，[属性の型]-[fullpath]を選択する ．
  3. 必要に応じてサイズを調整

※日本語のファイルパスは使用できません．

上手く調整すると以下のようになる．

参考サイト

なお，上記サイトではImportPhotosプラグインが使用されていましたが，QGIS3.28では動きませんでした．

Gist

gist9edf8ff48c8a64351994141b51d0bb9d

勉強会の議事メモ：2024/03/02

R

勉強会お疲れ様でした。

一般座標系平面二次元河床変動計算を書く

computational-sediment-hyd.hatenablog.jp

上記記事のパターン1をベースに検討を進める。

⇒ SIMPLE法を基本とした離散化を検討 ⇒ プリミティブ変数はv,hか？q,hでは対応できない。

小さなメッシュサイズおける浅水流計算の問題

computational-sediment-hyd.hatenablog.jp

⇒ close

スタッガードスキームは離散化方法の修正に対応可（別途書きます。）

AMR法（Adaptive Mesh Refinement、適合格子細分化法）

引き続き、文献収集を行う。

  • PARAMESHが参考になる？

備忘録：pythonでwebスクレイピング：プログラミングの筋トレ

R

導入

たまにやらないと忘れるので。簡単なスクレイピングの話です。

海上保安庁の潮汐推算のwebページのスクレイピングです。

データ公開ページ（例えば、https://www1.kaiho.mlit.go.jp/TIDE/pred2/cgi-bin/TidePredCgi.cgi?area=1603&back=../TidePred/tide_pred/2.htm&btn=ForAreaWindow_Japanese ）ですが、 なぜかボタンをクリックするとバグります。

pythonによるwebスクレイピング

pythonでのwebスクレイピングのコツは、

  • seleniumに頼らない。出来るだけbeautifulsoupを使う。
  • Chromeのデベロッパーツールでwebサイトをしっかり分析する。

くらいじゃないでしょうか。

それだけ、上のhtml内にタグで数値が埋め込まれているような化石サイトでも、下記のような短いコードでスクレイピングできます。

import pandas as pd
import numpy as np
from bs4 import BeautifulSoup
import requests

def getHarr(Area,Area2,year,month,day):
    url = f'https://www1.kaiho.mlit.go.jp/TIDE/pred2/cgi-bin/TidePredCgi.cgi?area={Area}&back=../TidePred/tide_pred/{Area2}.htm&year={year}&month={month}&day={day}&btn=%E6%8E%A8%E3%80%80%E7%AE%97'
    res = requests.get(url)
    soup = BeautifulSoup(res.content, 'html.parser')
    text = [t.get_text() for t in soup.findAll("td")]
    data = text[14:26] + text[40:52]
    # マイナス値の処理
    data = [d.replace(' ','') for d in data]
    return np.array(data, dtype=float)

%%time
Area = 1603
Area2 = 5
sdate = '2023/01/01'
edate = '2023/12/31'

val = [getHarr(Area, Area2, d.year, d.month, d.day) for d in pd.date_range(sdate, edate, freq='D')]
val = np.array(val).flatten()

df = pd.DataFrame(val
             , columns=[Area]
             , index=pd.date_range(sdate, periods=len(val), freq='H')
                 )

CPU times: total: 2min 16s
Wall time: 3min 49s
  • export
df.to_csv('tmp.csv', index_label='time')
  • export
df.plot()

Gist

gistd8b965fd743e0a46716787187dccfc82

Google Colab

※Colabの解説記事はこちら

Open In Colab

一次元浅水流計算における合流による水位上昇量の計算方法

R

本記事はGitHub、nbviewer、Colabでも公開しています。

※Colabの解説記事はこちら

a nbviewer Open In Colab

導入

「河道計画検討の手引き」に示される合流による水位上昇の計算方法について解説します。 この手法は、室田 明, 多田 博登:一次元水面形解析における合流点モデルに関する研究が元になっています。

計算式

合流による水位上昇量の計算方法の概要を以下に示す。

手引と同様に合流後河道の流向軸の運動量保存則は以下のとおりとなる。 コントロールボリュームの考え方が若干複雑なため、詳細は元論文を参考にされたい（時間ができたときにまとめます）。

\begin{align} & \beta \rho Q_2 \frac{Q_2}{B_2h_2}\cos \theta _2 + \beta \rho Q_1 \frac{Q_1}{B_1h_1}\cos \theta _1-\beta \rho Q_3 \frac{Q_3}{B_3h_3}\cos \theta _3 \\ & = B_3\frac{1}{2}\rho g {h_3}^2 - B'_2 \cos \theta _2 \frac{1}{2}\rho g {h_2}^2 - B'_1 \cos \theta _1 \frac{1}{2}\rho g {h_1}^2 \end{align}

ここに、\rho：水の密度、g：重力加速度、Q：流量、B：水路幅、h：水深、\theta：合流角度（下図参照）、\beta：運動量補正係数、B'：修正した川幅（下図参照）、添字1,2,3は河道1,2,3（下図参照、ここでは1：本川、2：支川とする）の諸量である。

元論文のとおりh_1=h_2を条件として式変形を行うと以下のとおりとなる。

\begin{align} &\left(\frac{B'_2}{B_3}\cos \theta _2 + \frac{B'_1}{B_3}\cos \theta _1\right)\left(\frac{h_1}{h_3}\right)^3-(1+2\beta {Fr}^2)\frac{h_1}{h_3}\\ &\hspace{20mm}+2 \beta \left\{\left(\frac{Q_2}{Q_3}\right)^2 \frac{B_3}{B_2}\cos \theta _2+\left(\frac{Q_1}{Q_3}\right)^2 \frac{B_3}{B_1}\cos \theta _1\right\}{Fr}^2=0\\ \end{align}

ここに、フルード数{Fr}^2=\dfrac{{Q_3}^2}{g{B_3}^2{h_3}^3}とする。

\begin{align} X&=\dfrac{h_1}{h_3}=\dfrac{h_2}{h_3}&\\ \alpha &= \left(\frac{B'_2}{B_3}\cos \theta _2 + \frac{B'_1}{B_3}\cos \theta _1\right)&\\ \gamma &= \left\{\left(\frac{Q_2}{Q_3}\right)^2 \frac{B_3}{B_2}\cos \theta _2+\left(\frac{Q_1}{Q_3}\right)^2 \frac{B_3}{B_1}\cos \theta _1\right\} \end{align}

として整理すると、

\begin{align} X^3-\frac{1+2\beta {Fr}^2}{\alpha}X+ \frac{2 \beta \gamma {Fr}^2}{\alpha}=0 \end{align}

のとおり、Xの三次方程式となる。これを解くことによって水位上昇量を計算する。

なお、元論文では\alpha=1（角度補正した合流前川幅の和が合流後川幅と等しい）を前提条件としているが、前出の手引には記載されていない。

本記事では簡易的に\alpha=1、\beta=1として水位上昇量Xの計算を行った。

テスト計算

計算モデル

  • 三次方程式はnp.rootsで解く。
  • 上記の解のうち、実数かつ1以上（水位上昇量のため）のものを水位上昇量とする。
  • 正しい条件を与えると解は1または0個になる。

参考 三次方程式の計算方法：https://west-village-tech.com/cubic_equation/

import numpy as np

def caldhConfluence(Q1Q3 ,Q2Q3 ,B3B1 ,B3B2 ,Theta1 ,Theta2 ,Fr):
    
    g = (Q2Q3)**2*B3B2*np.cos(Theta2*np.pi/180) \
     +  (Q1Q3)**2*B3B1*np.cos(Theta1*np.pi/180)
    
    x = np.roots([1,0,-1-2*Fr**2,2*g*Fr**2])
    
    # 実数のみ抽出
    x2 = x[np.iscomplex(x)==False]
    # 水位上昇量なので1以上のみ
    x3 = x2[np.where(x2>=1.0)]
    
    if len(x3) == 0:
        ans = np.nan
    elif len(x3) == 1:
        ans = x3[0].real
    else:
        print('error')
        ans = np.nan
    return ans

合流角度および合流前流量比の感度分析

合流角度は以下の3ケースを設定する。

\begin{align} \begin{array}{l:c:c} \mathrm{Case} & \theta_1[\mathrm{deg}] & \theta_2[\mathrm{deg}] \\ \hline \mathrm{Case A} & 10 & 10 \\ \mathrm{Case B} & 45 & 45 \\ \mathrm{Case C} & 0 & 90 \\ \end{array} \end{align}

合流前流量比は以下の3ケースを設定する。また、川幅はRegime theory(B = 5 \sqrt{Q})により設定する。よって、式中の係数は以下のとおりとなる。

\begin{align} \begin{array}{l:c:c:c:c:c} \mathrm{Case} & Q_1:Q_2 & Q_1/Q_3 & Q_2/Q_3 & B_3/B_1 & B_3/B_2 \\ \hline \mathrm{Case1} & 1:1 & 1/2 & 1/2 & \sqrt{2} & \sqrt{2} \\ \mathrm{Case2} & 2:1 & 2/3 & 1/3 & \sqrt{3/2} & \sqrt{3} \\ \mathrm{Case3} & 5:1 & 5/6 & 1/6 & \sqrt{6/5} & \sqrt{6} \\ \end{array} \end{align}

これらを組み合わせ9ケースについて合流後のフルード数を0.1～1.0まで変化させた場合の水位上昇量の計算結果を以下に示す。

これらより、以下の点が確認できる。

  • フルード数が大きい程水位上昇量が大きい
  • 合流角度が大きい程水位上昇量が大きい。（CaseA,B）
  • 合流流量比は1:1に近い程水位上昇量が大きい。
  • 直角合流CaseCの場合、合流流量が大きいCase1では水位上昇量は大きいが、Case3で相対的に水位上昇量が小さくなっている。
Fr = np.arange(0.1,1.01,0.1)

Q1Q3=1/2
Q2Q3=1/2
B3B1=np.sqrt(2)
B3B2=np.sqrt(2) 
dhoutA1 = [caldhConfluence(Q1Q3,Q2Q3,B3B1,B3B2,Theta1=10 ,Theta2=10 ,Fr=f) for f in Fr]
dhoutA2 = [caldhConfluence(Q1Q3,Q2Q3,B3B1,B3B2,Theta1=45 ,Theta2=45 ,Fr=f) for f in Fr]
dhoutA3 = [caldhConfluence(Q1Q3,Q2Q3,B3B1,B3B2,Theta1=0 ,Theta2=90 ,Fr=f) for f in Fr]

Q1Q3=2/3
Q2Q3=1/3
B3B1=np.sqrt(3/2)
B3B2=np.sqrt(3) 
dhoutB1 = [caldhConfluence(Q1Q3,Q2Q3,B3B1,B3B2,Theta1=10 ,Theta2=10 ,Fr=f) for f in Fr]
dhoutB2 = [caldhConfluence(Q1Q3,Q2Q3,B3B1,B3B2,Theta1=45 ,Theta2=45 ,Fr=f) for f in Fr]
dhoutB3 = [caldhConfluence(Q1Q3,Q2Q3,B3B1,B3B2,Theta1=0 ,Theta2=90 ,Fr=f) for f in Fr]

Q1Q3=5/6
Q2Q3=1/6
B3B1=np.sqrt(6/5)
B3B2=np.sqrt(6) 
dhoutC1 = [caldhConfluence(Q1Q3,Q2Q3,B3B1,B3B2,Theta1=10 ,Theta2=10 ,Fr=f) for f in Fr]
dhoutC2 = [caldhConfluence(Q1Q3,Q2Q3,B3B1,B3B2,Theta1=45 ,Theta2=45 ,Fr=f) for f in Fr]
dhoutC3 = [caldhConfluence(Q1Q3,Q2Q3,B3B1,B3B2,Theta1=0 ,Theta2=90 ,Fr=f) for f in Fr]

import matplotlib.pyplot as plt
import seaborn as sns
sns.set(context='paper', palette="bright", style="whitegrid", font_scale=0.9)

%matplotlib inline
fig = plt.figure(figsize=(5, 4), dpi=150)
ax = fig.add_subplot() 
ax.plot(Fr,dhoutA1, label='$ \\theta_1 =10,\\theta_2 =10, Q_1:Q_2=1:1$'         , c='b', ls='-')
ax.plot(Fr,dhoutA2, label='$ \\theta_1 =45,\\theta_2 =45, Q_1:Q_2=1:1$'         , c='g', ls='-')
ax.plot(Fr,dhoutA3, label='$ \\theta_1 = 0,\,\,\,\, \\theta_2 =90, Q_1:Q_2=1:1$', c='r', ls='-')

ax.plot(Fr,dhoutB1, label='$ \\theta_1 =10,\\theta_2 =10, Q_1:Q_2=2:1$'         , c='b', ls='--')
ax.plot(Fr,dhoutB2, label='$ \\theta_1 =45,\\theta_2 =45, Q_1:Q_2=2:1$'         , c='g', ls='--')
ax.plot(Fr,dhoutB3, label='$ \\theta_1 = 0,\,\,\,\, \\theta_2 =90, Q_1:Q_2=2:1$', c='r', ls='--')

ax.plot(Fr,dhoutC1, label='$ \\theta_1 =10,\\theta_2 =10, Q_1:Q_2=5:1$'         , c='b', ls=':')
ax.plot(Fr,dhoutC2, label='$ \\theta_1 =45,\\theta_2 =45, Q_1:Q_2=5:1$'         , c='g', ls=':')
ax.plot(Fr,dhoutC3, label='$ \\theta_1 = 0,\,\,\,\, \\theta_2 =90, Q_1:Q_2=5:1$', c='r', ls=':')

ax.set_xlabel('Froude number')
ax.set_ylabel('$X=h_1/h_3=h_2/h_3$')
# ax.set_title('[tex:Q\_1:Q\_2=1:1]')
ax.legend()
plt.show()

合流前川幅の感度分析

次に川幅の影響について感度分析を行った。

ケースとして、合流前川幅がRegime theory(B = 5 \sqrt{Q})の1.2倍、0.8倍を設定した。

式中の係数は以下のとおりとなる。ここでは、Q_1:Q_2=1:1のみとした。

\begin{align} \begin{array}{l:c:c:c:c:c} \mathrm{Case} & B_1,B_2 & Q_1:Q_2 & Q_1/Q_3 & Q_2/Q_3 & B_3/B_1 & B_3/B_2 \\ \hline \mathrm{Case I} & \mathrm{by\,Regime\,theory}\,\times\,1.0 & 1:1 & 1/2 & 1/2 & \sqrt{2} & \sqrt{2} \\ \mathrm{Case I\hspace{-1.2pt}I} & \mathrm{by\,Regime\,theory}\,\times\,1.2 & 1:1 & 1/2 & 1/2 & \dfrac{5\sqrt{2}}{6} & \dfrac{5\sqrt{2}}{6} \\ \mathrm{Case I\hspace{-1.2pt}I\hspace{-1.2pt}I} & \mathrm{by\,Regime\,theory}\,\times\,0.8 & 1:1 & 1/2 & 1/2 & \dfrac{5\sqrt{2}}{4} & \dfrac{5\sqrt{2}}{4} \\ \end{array} \end{align}

これらについて合流後のフルード数を0.1～1.0まで変化させた場合の水位上昇量の計算結果を以下に示す。

これらより、以下の点が確認できる。

  • 合流前川幅が大きいほど水位上昇量が大きくなる。これは流速が小さくなるためである。
  • 合流前川幅を小さくする場合、本計算条件では約0.7倍以下でXが1以下、つまり水位が上昇しない条件になる(本モデルではnanを返す)。これは、合流前の流れが射流になるためである。
Fr = np.arange(0.1,1.01,0.1)

Q1Q3=0.5
Q2Q3=0.5
B3B1=np.sqrt(2)
B3B2=np.sqrt(2)
dhout1 = [caldhConfluence(Q1Q3,Q2Q3,B3B1,B3B2,Theta1=10 ,Theta2=10 ,Fr=f) for f in Fr]

B3B1=5/6*np.sqrt(2)
B3B2=5/6*np.sqrt(2)
dhout2 = [caldhConfluence(Q1Q3,Q2Q3,B3B1,B3B2,Theta1=10 ,Theta2=10 ,Fr=f) for f in Fr]

B3B1=5/4*np.sqrt(2)
B3B2=5/4*np.sqrt(2)
dhout3 = [caldhConfluence(Q1Q3,Q2Q3,B3B1,B3B2,Theta1=10 ,Theta2=10 ,Fr=f) for f in Fr]

import matplotlib.pyplot as plt
import seaborn as sns
sns.set(context='paper', palette="bright", style="whitegrid", font_scale=0.9)

%matplotlib inline
fig = plt.figure(figsize=(5, 4), dpi=150)
ax = fig.add_subplot() 
ax.plot(Fr,dhout1, label='$\mathrm{by\,Regime\,theory}\, \\times \,1.0$')
ax.plot(Fr,dhout2, label='$\mathrm{by\,Regime\,theory}\, \\times \,1.2$')
ax.plot(Fr,dhout3, label='$\mathrm{by\,Regime\,theory}\, \\times \,0.8$')

ax.set_xlabel('Froude number')
ax.set_ylabel('$X=h_1/h_3=h_2/h_3$')
ax.set_title('[tex:Q\_1:Q\_2=1:1]')
ax.legend()
plt.show()

GitHub

github.com

参考文献

関連記事

computational-sediment-hyd.hatenablog.jp

備忘録：google Colabでcondaを使うためのライブラリ：condacolabの使い方

R

本記事はColabでも公開しています。

※Colabの解説記事はこちら

Open In Colab

https://pypi-camo.freetls.fastly.net/6cae3dec9a1e98ece1b184bd4863b26a0f73218d/68747470733a2f2f6769746875622e636f6d2f6a61696d657267702f636f6e6461636f6c61622f7261772f6d61696e2f636f6e6461636f6c61622e706e67

condacolabとは？

https://pypi.org/project/condacolab/(condacolab · PyPI]

Colabでcondaを使うためのライブラリです。

pythonではcondaによるインストールが推奨されるライブラリが多くあります。 Colabではpipが標準でcondaは準備されておりません。 Colabでconda環境を整備できなくはないですが、手間がかかる＆安定しません。 そのため、現時点（2024/2/10）ではcondacolabの使用が最適と思われます。

condacolabの使い方

公式https://pypi.org/project/condacolab/のとおりですが簡単にまとめておきます。

インストール

pipでインストールします。

!pip install -q condacolab
import condacolab

メソッド：condacolab.install

condacolab.installでconda環境を構築します。

以下のメソッドが準備されています。

  • 現時点（2024/2/10）ではpython3.10の環境が準備されています。pythonのバージョンは指定できないようです。
  • たまにColabがクラッシュすることがありますが再接続で解決します。

condacolab.install_miniconda()

Minicondaディストリビューションをインストールします。

condacolab.install_miniconda()

condacolab.install_miniforge()

Miniforgeディストリビューションをインストールします。 Miniforgeディストリビューションはconda-forgeによって公式に提供されています。

condacolab.install_miniforge()

condacolab.install_mambaforge()

推奨。Miniforgeのようなものですが、mambaが含まれています。Mambaforgeディストリビューションはconda-forgeによって公式に提供されています。

condacolab.install_mambaforge()

condacolab.install_anaconda()

Anacondaのフルパッケージをインストール？（未確認）

condacolab.install_anaconda()

condacolab.install_from_url()

スクリプトのURLを指定してインストール？（未確認）

condacolab.install()

condacolab.install_mambaforge()と同じ。

メソッド：condacolab.check

condaが正しくインストールされていることを確認する。

condacolab.check()

ライブラリのインストール

ディストリビューションのインストールが完了したら、通常のcondaと同様にライブラリをインストールします。

!conda install [package]

Gist

gista7996070dcafd41c23e421be4639ea5a