河川技術者向け基礎講座　準二次元不等流計算4/4：一般断面の不等流計算3-分割断面法+分割断面間の干渉を考慮（平均流速公式レベル3） - 趣味で計算流砂水理 Computational Sediment Hydraulics for Fun Learning

教科書の「不等流計算」は理解できるが、実務で汎用される「準二次元不等流計算」がなかなか理解し難い方に向けて、記事を書きました。多分相当わかりやすいと思いますので、河川行政に関わる方やコンサルの方に読んで頂きたいです。

全4回の第4回目です。

第1回：不等流計算の基礎
第2回：一般断面の不等流計算
第3回：一般断面の不等流計算2-分割断面法（平均流速公式レベル2）
第4回：一般断面の不等流計算3-分割断面法+分割断面間の干渉を考慮（平均流速公式レベル3）

本記事はGitHub、nbviewer、Colab、Marp（スライド形式）でも公開しています。

※Colabの解説記事はこちら

※Marpの解説記事はこちら

はじめに
分割断面間の干渉とは？
補足：斜昇流の存在
基礎式
限界水深、等流水深の定義
- 等流水深
- 限界水深
離散化
数値計算方法
本手法の課題
本手法の必要性、導入された経緯
まとめ
断面特性を計算するプログラム例
不等流計算のプログラム例
参考文献
関連記事

はじめに

前回説明した分割断面法（平均流速公式レベル2）では、分割断面間で流れの干渉は生じないこと条件とした。
今回説明する平均流速公式レベル3(以降、本手法)は、分割断面間での流れの干渉による運動量損失を考慮したモデルとなる。
流れ同士の干渉による損失と樹木群と流れの干渉による損失を考慮する。
種々の研究成果があるが、河道計画で広く使用されている福岡・藤田:複断面河道の抵抗予測と河道計画への応用の考え方を基本に説明を行なう。

おさらい
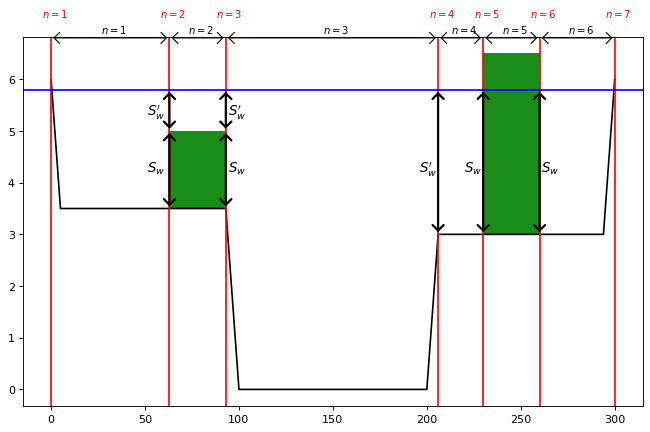
- 分割断面ごとに変わる：流速、河積、潤辺、粗度係数など
- 分割断面ごとに変わらない：水位、エネルギー勾配

分割断面間の干渉とは？

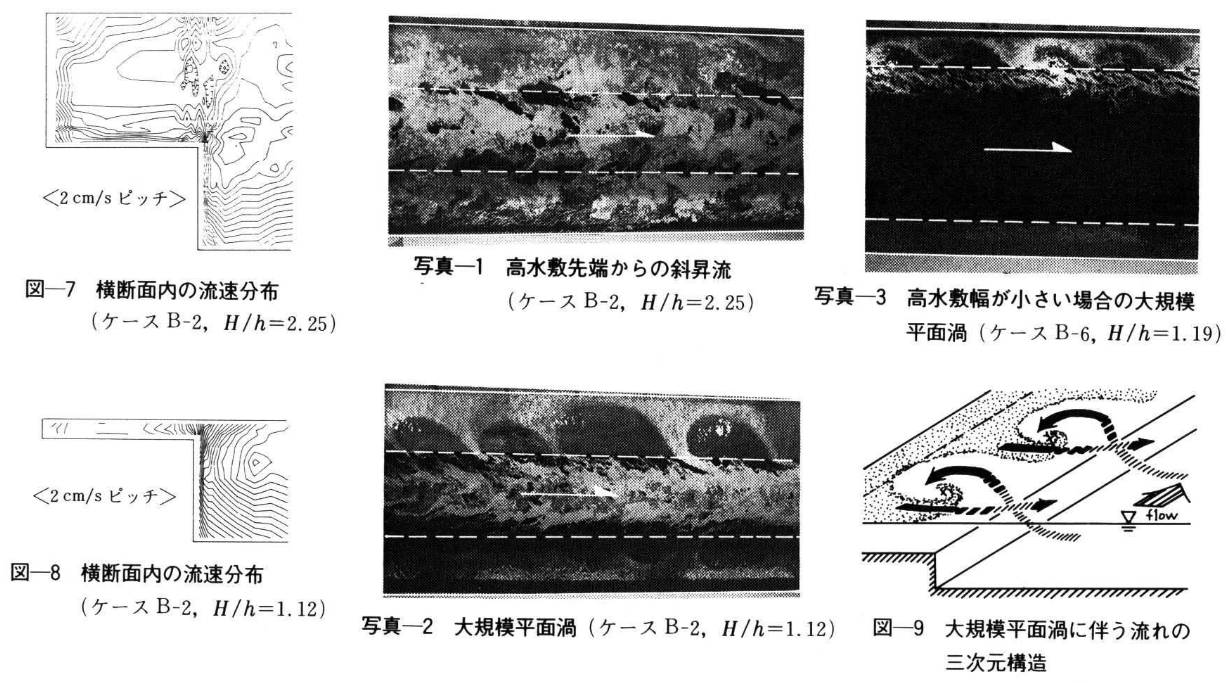
低水路・高水敷間など各領域の流速差が大きい場合、境界付近には水平渦が発生することが知られている。
本手法では、この渦による運動量損失が水位に影響を及ぼすと考えている。

石川ら,2011:洪水航空写真に捉えられた低水路河岸渦の特性に関する比較研究

前回講義でも少し説明したが、横断面内の流速分布は、高水敷・低水路間で不連続的となり、渦の影響を受けていることは明らかである。
実河川スケールでの観測データが少なく、その影響度合いは不明な点が多い。

福岡,藤田,1989:複断面河道の抵抗予測と河道計画への応用

補足：斜昇流の存在

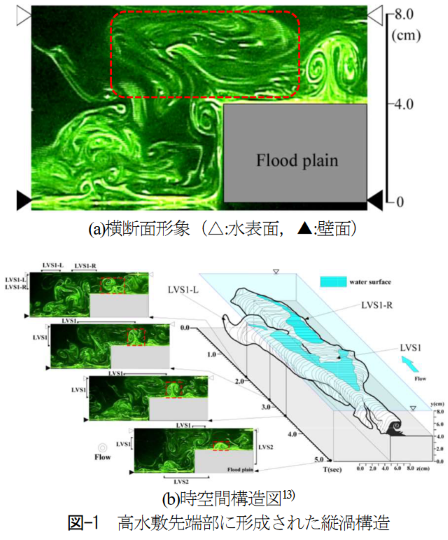
高水敷の流速が大きい場合、斜昇流と呼ばれる低水路から高水敷に向かう流れ(縦渦)が存在することが知られている。
今回説明する干渉の影響では、斜昇流による損失は考慮されていない。
観測、解析技術の進展により、徐々に実態が解明されつつある。実河川での観測例は無い（多分）。

渡辺ら2022:高水敷先端部の吸込み操作に伴う複断面開水路流れの変化特性

基礎式

運動方程式（流下方向）

本手法による不等流計算の運動方程式は次式を用いる。

$\begin{align} & \dfrac{d}{dx}\left( \frac{\beta Q^2}{2gA^2} + H \right) = -\dfrac{T}{\rho g A} \end{align}$

ここに、 $Q$ :流量、 $H$ ：水位、 $A=\sum A_n$ ：河積、 $T$ ：横断面全体の作用するせん断力、 $\beta$ ：運動量補正係数とする。

前回の分割断面法のときと同様である。今回は、右辺の生成項を変更を加える。

これまでは、生成項は河床の摩擦損失のみを考慮したが、本手法では、分割断面間の流れ同士の干渉による損失および樹木群と流れの干渉による損失を追加する。

これらを計算するためには各分割断面の流速が必要となる。次項に計算方法を示す。

横断方向の流速分布

各分割断面で流下方向に等流が成立すると仮定すると、各分割断面で次式が成り立つ。

$\begin{align} \dfrac{ T_n}{\rho g } = I A_n \end{align}$

ここで、分割断面間の流れ同士の干渉によるせん断力 $\tau^{\prime}$ (横断面の単位長さあたり)は次式で示す。

$\begin{align} \tau^{\prime} & = \rho f^{\prime} \Delta u |\Delta u | \end{align}$

また、樹木群と流れの干渉によるせん断力 $\tau$ (横断面の単位長さあたり)は次式で示す。

$\begin{align} \tau & = \rho f u^2 \end{align}$

ここに、 $\Delta u$ は境界面を介して隣り合う分割断面間での断面平均流速差、 $f,f^{\prime}$ は流れ間、流れと樹木間の境界混合係数とする。

河床摩擦損失はマニング則を用いて次式とする。

$\begin{align} I A_n = \dfrac{ {n}^2 {u}^2}{ {R}^{1/3} } {S} \end{align}$

具体例として、次の断面のうち、n=3と2の分割断面について運動方程式を立ててみる。

分割断面n=3の運動方程式

$\begin{align} \dfrac{ {n_n}^2 {u_n}^2}{ {R_n}^{1/3} } {S_n} +\dfrac{ \tau_n {S_w}_n}{\rho g} + \dfrac{ \tau^{\prime}_n {S^{\prime}_w}_n + \tau^{\prime}_{n+1} {S^{\prime}_w}_{n+1} }{\rho g} & = A_n I \\ \tau_n &= \rho f_n u_n^2 \\ \tau^{\prime}_n &= \rho f^{\prime}_n \Delta u |\Delta u | = \rho f^{\prime}_n (u_n-u_{n-1}) |u_n-u_{n-1}| \\ \tau^{\prime}_{n+1} &= \rho f^{\prime}_{n+1} \Delta u |\Delta u | = \rho f^{\prime}_{n+1} (u_n-u_{n+1}) |u_n-u_{n+1}| \end{align}$

分割断面n=2の運動方程式

$\begin{align} \dfrac{ {n_n}^2 {u_n}^2}{ {R_n}^{1/3} } {S_n} + \dfrac{ \tau^{\prime}_n {S^{\prime}_w}_n + \tau^{\prime}_{n+1} {S^{\prime}_w}_{n+1} }{\rho g} & = A_n I \\ \tau^{\prime}_n &= \rho f^{\prime}_n \Delta u |\Delta u | = \rho f^{\prime}_n (u_n-u_{n-1}) |u_n-u_{n-1}| \\ \tau^{\prime}_{n+1} &= \rho f^{\prime}_{n+1} \Delta u |\Delta u | = \rho f^{\prime}_{n+1} (u_n-u_{n+1}) |u_n-u_{n+1}| \end{align}$

すべての分割断面に対応できるように、一般化すると次式となる。

$\begin{align} \dfrac{ {n_n}^2 {u_n}^2}{ {R_n}^{1/3} } {S_n} +\dfrac{ \tau_n {S_w}_n + \tau_{n+1} {S_w}_{n+1}}{\rho g} + \dfrac{ \tau^{\prime}_n {S^{\prime}_w}_n + \tau^{\prime}_{n+1} {S^{\prime}_w}_{n+1} }{\rho g} & = A_n I \\ \tau_n &= \rho f_n u_n^2 \\ \tau_{n+1} &= \rho f_{n+1} u_n^2 \\ \tau^{\prime}_n &= \rho f^{\prime}_n \Delta u |\Delta u | = \rho f^{\prime}_n (u_n-u_{n-1}) |u_n-u_{n-1}| \\ \tau^{\prime}_{n+1} &= \rho f^{\prime}_{n+1} \Delta u |\Delta u | = \rho f^{\prime}_{n+1} (u_n-u_{n+1}) |u_n-u_{n+1}| \end{align}$

よって、分割断面の数だけ方程式が成立する。なお、分割断面n=5は流速0のため、これを除いた5分割断面の計算を行なう。

さらに、以下の連続式を連立させることにより、各分割断面の流速と損失勾配 $I$ を同時に解くことができる。

$\begin{align} Q = \displaystyle \sum^n {u_n}A_n \end{align}$

ここで得られた流速から求めるせん断力を流下方向の運動方程式に代入することにより縦断水位を計算する。なお、流水間のせん断力は前述のとおり分割断面間でキャンセルされるため、計算しないことに留意する。

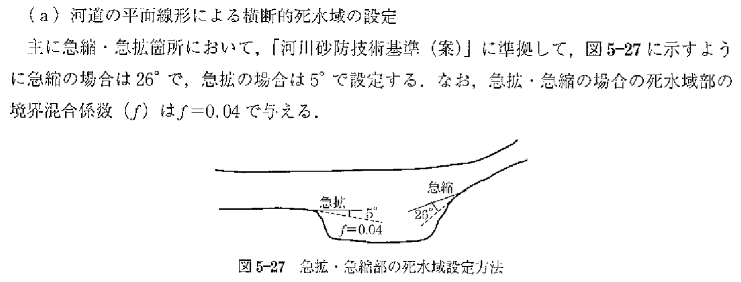
さらに、以下のように有効断面の外側に死水域を設定する場合は下式のように境界部分のせん断力を考慮する。

$\begin{align} \dfrac{T}{\rho g A} = \dfrac{1}{A}\left( \sum_n^{nmax} \left( \dfrac{ {n_n}^2 {u_n}^2}{ {R_n}^{1/3} } {S_n} \right) + \sum_n^{nmax+1} \left( \dfrac{ \tau_n {S_w}_n}{\rho g} \right) + \dfrac{\tau^{\prime}_0 {S^{\prime}_w}_0}{\rho g} + \dfrac{\tau^{\prime}_{nmax+1} {S^{\prime}_w}_{nmax+1}}{\rho g} \right) \end{align}$

河道計画検討の手引き

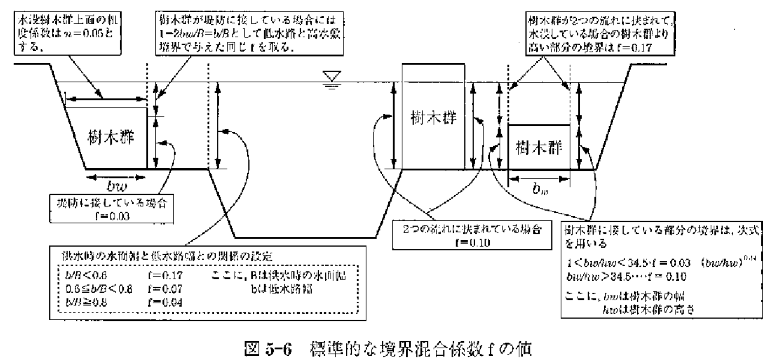
境界混合係数について

境界混合係数の標準値は以下のように定義されている。

私の感覚では厳密にこの図に則って計算している事例は少ないように思う。高水敷・低水路間だけしっかり決めてあげれば良い気がする。

河道計画検討の手引き

限界水深、等流水深の定義

一般断面の基礎式を用いて、限界水深、等流水深を矩形断面と同様に定義で設定することは難しいため、便宜的に以下のとおりに設定する。

等流水深

全ての損失による水頭の勾配が河床勾配 $i_b$ と釣り合う状態を等流と定義してその水深を等流水深とする。なお、一般断面では水深を用いないため、正確には等流時の水位となる。

$\begin{align} \dfrac{T}{\rho g A} = i_b \end{align}$

となり、これを満足する水位 $H$ を反復法などにより求めれば良い。

限界水深

フルード数が1となる水位を限界流時の水位とする。

フルード数はエネルギー保存則の分母が0より、

$\begin{align} 1 &= \dfrac{\alpha q^2}{gh^3} \\ Fr&= \dfrac{V}{ \sqrt{\dfrac{gh}{\alpha}}} \\ Fr&= \dfrac{Q}{A\sqrt{\dfrac{gh}{\alpha}} } \end{align}$

となるが、平方根の中に水深 $h$ が含まれるため、一般断面ではそのままでは計算できない。

そのため、分割断面法では水深 $h$ の代替として井田の合成径深 $R_c$ を使用することが多い。その他には径深 $R=A/S$ 、 $A/B$ を用いることもある。

参考：FORUM8ソフトウェア：等流・不等流の計算・3DCAD Ver.9 Q&A

離散化

横断方向流速分布の式は以下となり、分割断面数分の式が成り立つ。

以下の連続式を連立させることにより、各分割断面の流速と損失勾配 $I$ を求める。

$\begin{align} Q = \displaystyle \sum^n {u_n}A_n \end{align}$

縦断水位の離散化はこれまでと同様に次式となる。なお、 $i$ :上流側、 $i-1$ :下流側とする。

$\begin{align} \left(\frac{\beta_i Q^2}{2gA^2_i} + H_i \right) -\left( \frac{\beta_{i-1} Q^2}{2gA_{i-1}^2} + H_{i-1} \right) &= \dfrac{1}{2}\left(\dfrac{T_i}{\rho g A_i} + \dfrac{T_{i-1}}{\rho g A_{i-1}} \right)\Delta x \\ A&=\sum A_n \end{align}$

常流の場合、下流から逐次計算を行なうため未知数は $H_i$ のみとなる。

数値計算方法

縦断水位はこれまで同様のため説明を省略し、横断方向流速分布の計算方法をのみを示す。この計算にはかなり高度な数値計算手法が必要なため、理解できなくても問題ない。

計算するための前知識として以下の2手法を紹介する。

手法1：高次のニュートン法

高次のニュートン法は、通常のニュートン法と同様に以下のように示される。なお、ボールド体は行列を示す。

$\begin{align} \boldsymbol{X}^{n+1}&=\boldsymbol{X}^{n} -\frac{\partial \boldsymbol{f}(\boldsymbol{X}^n)}{\partial\boldsymbol{X}}^{-1}\boldsymbol{f}(\boldsymbol{X}^n) \end{align}$

上式の右辺第二項を $\boldsymbol{r}$ とおく。

$\begin{align} \boldsymbol{r}&=\frac{\partial \boldsymbol{f}(\boldsymbol{X}^n)}{\partial \boldsymbol{ X}}^{-1}\boldsymbol{f}(\boldsymbol{ X}^n) \end{align}$

$\boldsymbol{r}$ は $\dfrac{\partial \boldsymbol{f}( \boldsymbol{X}^n)}{\partial \boldsymbol{X}}$ の逆行列が計算できれば、容易に求めることができる。

よって、下式で解の更新を行なう。

$\begin{align} \boldsymbol{X}^{n+1}&=\boldsymbol{X}^{n}-\boldsymbol{r} \end{align}$

手法2：TDMA法

TDMA法（トーマス法）とは係数行列が三重対角行列の連立一次元方程式の効率的な数値解法である。ガウスの消去法(直接法)の計算量は分割数Nの3乗であるが、TDMA法はNの数倍程度の計算量となる。

導出はwikipediaを参照ください。https://en.wikipedia.org/wiki/Tridiagonal_matrix_algorithm

def TDMA(a,b,c,d):
    x, P, Q = np.empty_like(a), np.empty_like(a), np.empty_like(a)
    n = len(x)
    
    P[0], Q[0] = -c[0]/b[0], d[0]/b[0]
    for i in range(1, n):
        P[i] = -  c[i]                /(a[i]*P[i-1] + b[i])
        Q[i] =  (-a[i]*Q[i-1] + d[i])/(a[i]*P[i-1] + b[i])
        
    x[-1] = Q[-1]
    for i in range(n-2, -1, -1):
        x[i] = P[i]*x[i+1] + Q[i]
        
    return x

大規模演算に使用することを意識するとメモリ節約版も知っておくと良い。引数をそのまま使うため、参照渡しの場合、引数の値が変わることに注意

参考： https://nekodamashi-math.blog.ss-blog.jp/2017-12-03-2

def lmTDMA(a,b,c,d):
    n = len(a)
    #! 前進消去
    for i in range(1, n):
        ratio=a[i]/b[i-1]
        b[i]=b[i] - ratio*c[i-1]
        d[i]=d[i] - ratio*d[i-1]

    #! 後退代入
    d[-1]=d[-1]/b[-1]
    for i in range(n-2, -1, -1):
        d[i]=(d[i]-c[i]*d[i+1])/b[i]

    return d

計算方法

分割断面の運動方程式を $u$ について展開する。

以下のとおりに式変形できる。

$\begin{align} a_n X_{n-1}+b_n X_{n}+c_n X_{n+1}-A_n=0 \end{align}$

ここに、

$\begin{align} X_n&=\dfrac{u_n}{\sqrt{I}} \\ a_n&=-\frac{\rho {f^{\prime}}_{n} {S^{\prime}_w}_{n}(X_{n}-X_{n-1}) \sigma_1} {\rho g}\\ b_n&=\left\lbrace \frac{ {n_n}^2 }{ {R_n}^{1/3} } {S}_n +\frac{ \rho {f}_{n} {S_w}_{n}+\rho {f}_{n+1} {S_w}_{n+1}}{\rho g}\right\rbrace X_n - a_n - c_n \\ c_n&=-\frac{\rho {f^{\prime}}_{n+1} {S^{\prime}_w}_{n+1}(X_{n}-X_{n+1}) \sigma_2} {\rho g}\\ \sigma_1 & = \dfrac{(u_n-u_{n-1})}{|u_n-u_{n-1}|} \\ \sigma_2 & = \dfrac{(u_n-u_{n+1})}{|u_n-u_{n+1}|} \end{align}$

全分割断面の方程式をベクトル形式で記述すると以下となる。なお、分割断面5は、水深が0となるため、省いて行列を構成する。

$\begin{align} \boldsymbol{X}=\dfrac{1}{\sqrt{I}} \begin{pmatrix} u_1 \\ u_2 \\ u_3 \\ u_4 \\ u_6 \\ \end{pmatrix} \end{align}$

$\begin{align} \boldsymbol{\alpha(\boldsymbol{X})}= \begin{pmatrix} b_1 && c_1 && 0 && 0 && 0 \\ a_2 && b_2 && c_2 && 0 && 0 \\ 0 && a_3 && b_3 && c_3 && 0 \\ 0 && 0 && a_4 && b_4 && c_4 \\ 0 && 0 && 0 && a_6 && b_6 \\ \end{pmatrix} \end{align}$

$\begin{align} \boldsymbol{\beta}= \begin{pmatrix} A_1 \\ A_2 \\ A_3 \\ A_4 \\ A_6 \\ \end{pmatrix} \end{align}$

$\begin{align} \boldsymbol{f}(\boldsymbol{X})= \boldsymbol{\alpha(\boldsymbol{X})}\boldsymbol{X} - \boldsymbol{\beta} \end{align}$

$\boldsymbol{\alpha}$ は $X$ の関数のため、直接計算することができない。

そのため、高次のニュートン法を用いて反復計算を行なう。 $\boldsymbol{f}$ の微分式は以下となる。

$\begin{align} \frac{\partial \boldsymbol{f}(\boldsymbol{X})}{\partial \boldsymbol{X}}= \begin{pmatrix} 2b_1 && 2c_1 && 0 && 0 && 0 \\ 2a_2 && 2b_2 && 2c_2 && 0 && 0 \\ 0 && 2a_3 && 2b_3 && 2c_3 && 0 \\ 0 && 0 && 2a_4 && 2b_4 && 2c_4 \\ 0 && 0 && 0 && 2a_6 && 2b_6 \\ \end{pmatrix} \end{align}$

なお、上式は三重対角行列となるため、TDMAにより容易に逆行列が計算可能である。

ニュートン法による計算結果の $\boldsymbol{X}$ と以下の連続式を連立させる。

$\begin{align} Q = \displaystyle \sum^n {u_n}A_n \end{align}$

よって、以下の式により $\sqrt{I}$ , $u_j$ を求める。

$\begin{align} \sqrt{I}&=\frac{Q}{ \displaystyle \sum_n (X_n A_n)} \\ u_n&=\sqrt{I}\cdot X_n \end{align}$

本手法の課題

境界混合係数が大きすぎる
- 境界混合係数は高水敷、低水路の区分が明確な大河川での水平渦を想定して設定された値である。そのため、適用範囲は限定的。
- それにも関わらず、直轄河川では汎用されており、過大評価と考えられる。
樹木群の死水域設定
- 洪水流をみればわかるが、完全に死水域となる樹木群はほとんどない。
- 実務では樹木群を死水域として取り扱うことが慣習化されており、過大評価と言える。

上記からわかるとおり、本手法では水位が高めに計算されがちである。

本手法の必要性、導入された経緯

福岡、藤田、山本などによると、
- 当時は痕跡水位から粗度係数を逆算することが行われており、様々な抵抗が粗度係数に含まれていた。
- マニング則は、河床の摩擦抵抗を示した式であり、それ以外の抵抗は当然評価できない。
- このような現象に基づかない計画は見直したい。つまり、流れの抵抗を適切に評価する必要がある。
福岡、藤田は、流れの干渉、流れと樹木群の干渉に着目し、本手法を提案した。
余談ですが、山本は低水路の粗度係数に着目し、流況と河床波の関係から粗度係数を評価する方法提案した。つまり、粗度係数は物理定数であることを改めて示した。
- 河道計画検討の手引から、低水路の粗度係数の設定に重点を置いていることが理解できる。
- 基本的には、推定粗度（流況によって決まる粗度）を使うことになっている。(未経験の出水に対して合理的に粗度係数を決める)
- これらの知見は、半理論式と現地観測（涸沼川での河床波計測など）から見出されたが外挿も多く、不明な点が多い。

本手法には多くの問題点あるが、より正確に水位を計算したいという考えは正しいと思われる。

まとめ

本手法：平均流速レベル3による一次元（準二次元）不等流計算方法について説明を行った。

直轄河川の流下能力評価を行なう方は、本手法の概要くらいは理解して欲しい。
数値計算方法はかなり難しいので理解できなくても問題ない。
複断面河道の水理は、かつて世界的に様々な研究がなされたため、興味のある方は参照すると面白い。
複断面河道の詳細な流況はまだまだ不明な点も多く、近年でも特に実験に関する研究成果が見られる。

断面特性を計算するプログラム例

ボリュームがあるため、別ページに作成

不等流計算のプログラム例

ボリュームがあるため、別ページに作成

参考文献

リンク

jupyterをはてブロのmarkdownに変換

computational-sediment-hyd.hatenablog.jp

はじめに

分割断面間の干渉とは？

補足：斜昇流の存在

基礎式

運動方程式（流下方向）

横断方向の流速分布

境界混合係数について

限界水深、等流水深の定義

等流水深

限界水深

離散化

数値計算方法

手法1：高次のニュートン法

手法2：TDMA法

計算方法

本手法の課題

本手法の必要性、導入された経緯

まとめ

断面特性を計算するプログラム例

不等流計算のプログラム例

参考文献

関連記事