河川技術者向け基礎講座　準二次元不等流計算1/4：不等流計算の基礎 - 趣味で計算流砂水理 Computational Sediment Hydraulics for Fun Learning

教科書の「不等流計算」は理解できるが、実務で汎用される「準二次元不等流計算」がなかなか理解し難い方に向けて、記事を書きました。多分相当わかりやすいと思いますので、河川行政に関わる方やコンサルの方に読んで頂きたいです。

全4回の第1回目です。

第1回：不等流計算の基礎
第2回：一般断面の不等流計算
第3回：一般断面の不等流計算2-分割断面法（平均流速公式レベル2）
第4回：一般断面の不等流計算3-分割断面法+分割断面間の干渉を考慮（平均流速公式レベル3）

本記事はGitHub、nbviewer、Colab、Marp（スライド形式）でも公開しています。

※Colabの解説記事はこちら

※Marpの解説記事はこちら

基礎式
離散化
水面形方程式
- 水面形の追跡方向
- 水面形の概形
数値計算方法
サンプルコード
補足：常流、射流混在流れの数値計算方法
参考文献
関連記事

基礎式

矩形近似した断面の不等流計算の基礎式はベルヌーイの式とマニング則より次式となる。

$\begin{align} & \dfrac{d}{dx}\left( \frac{q^2}{2gh^2} + h + z_b \right) = -i_e \\ & q = \dfrac{1}{n}i_e^{1/2}h^{5/3} \\ \end{align}$

ここに、 $q$ :単位幅流量、 $h$ ：水深、 $z_b$ ：河床高、 $i_e$ ：エネルギー勾配、 $n$ ：マニングの粗度係数、 $g$ ：重力加速度とする。

等流水深 $h_0$ 、限界水深 $h_c$ は次式となる。

$\begin{align} h_0&=\left(\dfrac{q^2n^2}{i_b}\right)^{3/10} \\ h_c&=\left(\dfrac{q^2}{g}\right)^{1/3} \end{align}$

ここに、 $i_b = - \dfrac{d z_b}{dx}$ ：河床勾配とする。

離散化

ベルヌーイの式とマニング則を連立させて離散化すると次式となる。なお、 $i$ :上流側、 $i-1$ :下流側とする。

$\begin{align} \left(\frac{q^2}{2gh^2_i} + h_i + {z_b}_i \right) -\left( \frac{q^2}{2gh_{i-1}^2} + h_{i-1} + {z_b}_{i-1} \right) = \dfrac{1}{2}\left(\dfrac{q^2n^2}{h_i^{10/3}} + \dfrac{q^2n^2}{h_{i-1}^{10/3}}\right)\Delta x \end{align}$

エネルギー勾配は上下流断面の平均値を用いている。

常流の場合、下流から逐次計算を行なうため未知数は $h_i$ のみとなる。

水面形方程式

前出のベルヌーイの式を変形して次の水面形方程式（水深の微分に関する方程式）を得る。

$\begin{align} \dfrac{d}{dx}\left( \dfrac{q^2}{2gh^2} + h + z_b \right) &= -i_e \\ - \dfrac{q^2}{gh^3}\dfrac{dh}{dx} + \dfrac{dh}{dx} + \dfrac{d z_b}{dx} &= -i_e \\ \dfrac{dh}{dx} &= \dfrac{i_b -i_e }{ 1 - \dfrac{q^2}{gh^3}} \\ &= \dfrac{i_b -i_e }{ 1 - {Fr}^2} \end{align}$

ここに、 $Fr = \dfrac{v}{\sqrt{gh}} = \dfrac{q}{\sqrt{gh^3}}$ ：フルード数とする。

水面形方程式の分子=0は $\dfrac{dh}{dx}=0$ のため等流状態を示し、前出の等流水深が得られる（等流水深の定義）。また、分母=0から限界水深が得られ（限界水深の定義）、 $\dfrac{dh}{dx}=\infty$ のため水面形が得られない。この地点は支配断面と呼ばれる。

上式を $h_0,h_c$ を用いて展開すると次式が得られる。（式展開は例えばここを参照）

$\begin{align} \dfrac{dh}{dx} &= i_b \dfrac{1-\left(\dfrac{h_0}{h}\right)^{10/3}}{1-\left(\dfrac{h_c}{h}\right)^3 } \end{align}$

不等流計算を行なう上で本式より以下を理解しておく必要がある。

水面形の追跡方向

$Fr \lt 1$ または $h_c \lt h$ または $v\lt\sqrt{gh}$ は、常流
$Fr \gt 1$ または $h_c \gt h$ または $v\gt\sqrt{gh}$ は、射流

と定義される。 $\sqrt{gh}$ は（微小振幅波理論による水面波の）波速であり、射流は $v\gt\sqrt{gh}$ のため水面変化が下流のみに影響するが、常流では上流にも影響をすることが示されている。そのため、不等流計算の水面形の追跡方向は、常流は下流から上流、射流は上流から下流となる。

水面形の概形

$h,h_0,h_c$ の関係より $\dfrac{dh}{dx}$ の符号が決まるため水面形の概形が把握できる。教科書にみられる緩勾配水路（M水路、 $h_0 \gt h_c$ ）や急勾配水路（S水路、 $h_0 \lt h_c$ ）などの水面形はこの考え方による描くことができる。

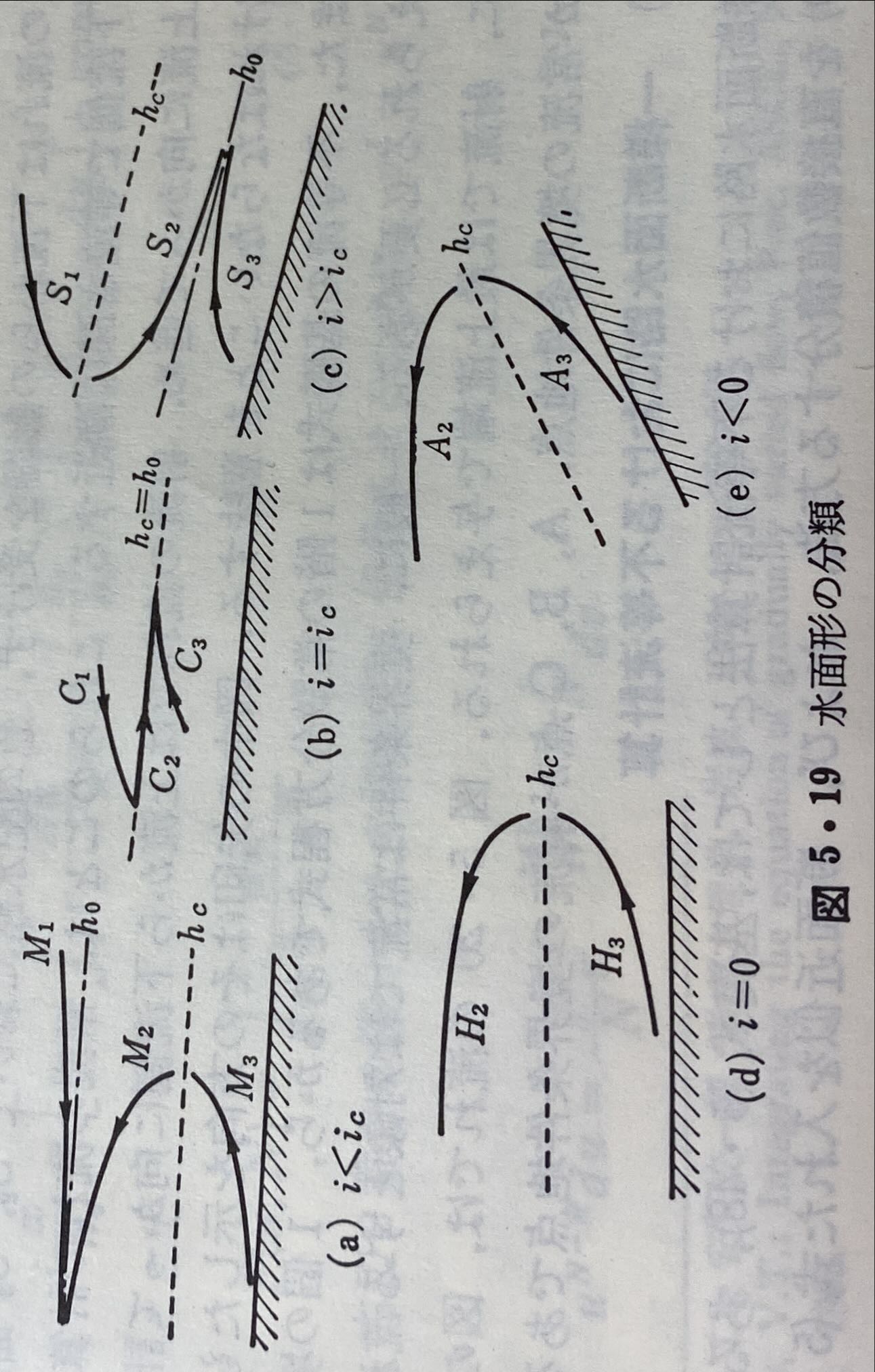
出典：椿東一郎水理学1 pp.151

数値計算方法

未知数 $h_i$ は直接計算できなため反復法によって近似解を求める。ここでは、ニュートン法を用いた。（参考：ニュートン法とは）

ニュートン法のアルゴリズムに沿うと、計算式は次のとおりとなる。

$\begin{align} f &= \left(\frac{q^2}{2gh^2_i} + h_i + {z_b}_i \right) -\left( \frac{q^2}{2gh_{i-1}^2} + h_{i-1} + {z_b}_{i-1} \right) - \dfrac{1}{2}\left(\dfrac{q^2n^2}{h_i^{10/3}} + \dfrac{q^2n^2}{h_{i-1}^{10/3}}\right)\Delta x \\ \dfrac{df}{dh_i} &= -\frac{q^2}{gh^3_i} + 1 + \dfrac{5}{3}\dfrac{q^2n^2}{h_i^{13/3}} \Delta x \end{align}$

$\begin{align} h^{new}_i &= h_i - \dfrac{f}{\dfrac{df}{dh_i}} % f &= \left(\frac{q^2}{2gh^2_i} + h_i + {z_b}_i \right) % -\left( \frac{q^2}{2gh_{i-1}^2} + h_{i-1} + {z_b}_{i-1} \right) % + \dfrac{1}{2}\left(\dfrac{q^2n^2}{h_i^{10/3}} + \dfrac{q^2n^2}{h_{i-1}^{10/3}}\right)\Delta x \\ % \dfrac{df}{dh_i} &= -\frac{q^2}{gh^3_i} + 1 % - \dfrac{5}{3}\dfrac{q^2n^2}{h_i^{13/3}} \Delta x \end{align}$

サンプルコード

単位幅流量0.5 $\mathrm{m^3/s/m}$ 、マニングの粗度係数0.02、河床勾配1/500、水路延長50 $\mathrm{m}$ の矩形水路を対象に下流端水位を限界水深としたときの水面形を計算せよ。なお、 $\Delta x$ は0.1 $\mathrm{m}$ とする。

import numpy as np

q = 0.5
n = 0.02
ib = 1/500
g = 9.8
dx = 0.1

h0 = (q**2*n**2/ib)**0.3 #等流水深
hc = (q**2/g)**(1/3) # 限界水深

L = np.arange(0,50.01,dx) #追加距離の配列
zb = L*ib #河床高の配列
h = np.zeros_like(L) #水深の配列

h[0] = hc #下流端条件
for i in range(1,len(h)):
    h[i] = h[i-1] #収束計算の初期値：一つ下流側の断面の水深
    f = 1.0 #仮値
    dfdh = 1.0 #仮値
    while np.abs(f/dfdh) > 10**(-8): # 反復計算の収束条件
        f = q**2/2.0/g/h[i]**2 + h[i] + zb[i] \
          -(q**2/2.0/g/h[i-1]**2 + h[i-1] + zb[i-1]) \
          - 0.5*(q**2*n**2/h[i]**(10/3) + q**2*n**2/h[i-1]**(10/3))*dx
        dfdh = -q**2/g/h[i]**3 + 1 + 5/3*q**2*n**2/h[i]**(13/3)*dx
        h[i] -= f/dfdh

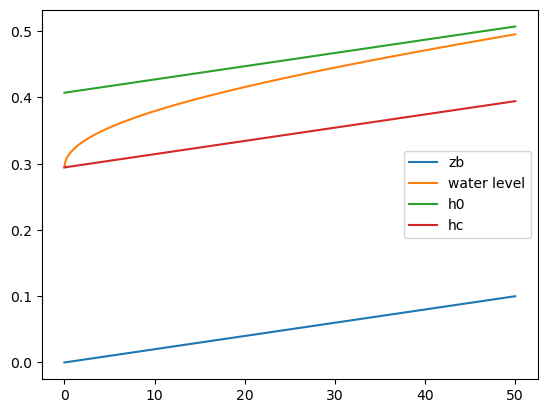
import matplotlib.pyplot as plt

plt.plot(L,zb, label='zb')
plt.plot(L,h+zb, label='water level')
plt.plot(L,zb+h0, label='h0')
plt.plot(L,zb+hc, label='hc')
plt.legend()              # 凡例の表示
plt.show()                # 描画