掃流砂量と川幅の関係について + 問題提起：流砂量式の関数形について - 趣味で計算流砂水理 Computational Sediment Hydraulics for Fun Learning

本記事はGitHub、nbviewer、Colabでも公開しています。

※Colabの解説記事はこちら

モチベーション
前提条件
川幅～水深～無次元掃流力の関係
川幅、水深、無次元掃流力と掃流砂量の関係
- 式の導出
- 計算結果
おまけ：MPM式（1.5乗則）の奇妙な特性
GitHub
参考図書
関連記事

モチベーション

河道改修等によって川幅を広げると、流速および摩擦速度は小さくなる一方で掃流幅（掃流砂が流れる川幅）は大きくなります。その場合、掃流砂量がどのように変化するかが気になったため簡単な検証を行いました。

前提条件

簡単のため、矩形近似断面による等流計算を用いた数値実験を行いました。

まず、以下の4点の仮定を設定します。

流量は河道改修前後で変わらない
河床勾配は河道改修前後で変わらない
河床材料の粒径は河道改修前後で変わらない
河床抵抗係数（マニングの粗度係数）は河道改修前後で変わらない

1点目は違和感はないと思いますが、それ以外は長期的には変化する可能性がありますので、今回の数値実験はあくまでも河道改修直後の変化をイメージしています。

与条件としては、現況河道の川幅、水深および無次元掃流力（=0.06）を与えます。

川幅～水深～無次元掃流力の関係

式の導出

前項の条件に基づき、河道改修前後で変化しない諸量を用いて以下の指標を設定します。

$\begin{align} X &= \dfrac{d}{i_b} \\ Y &= \dfrac{nQ}{\sqrt{i_b}} \end{align}$

これを用いると、無次元掃流力は次式で示されます。

$\begin{align} \tau_*= \dfrac{h i_b}{\rho_{sw}d} = \dfrac{h }{\rho_{sw} X} \end{align}$

ここで、無次元掃流力を砂礫の移動限界を考慮して0.05～0.5の範囲で与えたとすると、水深は次式で示すことができます。

$\begin{align} h = \tau_* \rho_{sw} X \end{align}$

一方、川幅はマニング則を用いると以下のようになります。

$\begin{align} Q &= \dfrac{1}{n}\sqrt{i_b}h^{5/3}B \\ B &=\dfrac{nQ}{\sqrt{i_b} h^{5/3}} = \dfrac{Y}{h^{5/3}} = \dfrac{Y}{(\tau_* \rho_{sw} X)^{5/3}} \end{align}$

計算手順

与条件（現況河道の川幅、水深および無次元掃流力）より $X,Y$ を計算する。

$\begin{align} X &= \dfrac{d}{i_b} = \dfrac{h }{\rho_{sw} \tau_*} \\ Y &= \dfrac{nQ}{\sqrt{i_b}} = h^{5/3}B \end{align}$

$X,Y$ を用いて、無次元掃流力0.05～0.5の場合の水深、川幅を求める。

計算結果

与条件は、以下の2ケースを設定します。

現況川幅100m、水深3.0m
現況川幅200m、水深7.0m

以下のコードのとおり計算を行いました。

import numpy as np

# parameters
g = 9.8
rhosw = 1.65 # grain specific gravity in water

# conditions
tss = 0.06
hst = 3.0
Bst = 100.0

lts = np.linspace(0.05,0.5,50,endpoint=True)

# case1
hst = 3.0
Bst = 100.0
# 基準値より逆算
diByib = hst/rhosw/tss
nQBySqIb = hst**(5/3)*Bst

lh = lts*rhosw*diByib
lB = nQBySqIb/lh**(5/3)

# case2
hst = 7.0
Bst = 200.0
# 基準値より逆算
diByib = hst/rhosw/tss
nQBySqIb = hst**(5/3)*Bst

lh2 = lts*rhosw*diByib
lB2 = nQBySqIb/lh2**(5/3)

計算結果より、無次元掃流力~川幅、無次元掃流力~水深、川幅~水深の関係を次図に示します。

自明ですが、川幅の増加により水深は減少します。
一方、無次元掃流力は川幅に対して負の相関、水深に対して正の相関を示してます。
また、与条件の差異による2ケースは、すべての関係で相似形を示しています。そのため、次項ではケース1のみを検討します。

川幅、水深、無次元掃流力と掃流砂量の関係

式の導出

掃流砂量式として、比較的簡単な式形を示すBrown式、MPM式を使用します。 2式による無次元掃流砂量は以下のとおりです。

Brown式

$\begin{align} q_{b*}= \frac{q_b}{\sqrt{\rho_{sw} g d^3}}=10 \tau_*^{\frac{5}{2}} \end{align}$

MPM式

$\begin{align} q_{b*}= \frac{q_b}{\sqrt{\rho_{sw} g d^3}}=8 (\tau_* - \tau_{*c})^{\frac{3}{2}} \end{align}$

なお、MPM式の限界無次元掃流力 $\tau_{*c}$ は0.05とします。

これらを用いると横断面全体の掃流砂量は次式で定義できます。

$\begin{align} Q_b &= B q_{b} = B \sqrt{\rho_{sw} g d^3}q_{b*} \end{align}$

本検討では粒径を定義していないため、掃流砂量を粒径で除した次式を基準掃流砂量とします。

$\begin{align} \dfrac{Q_b}{d^{1.5}} &= B \sqrt{\rho_{sw} g}q_{b*} \end{align}$

また、確認のため、単位幅形式でも示しておきます。

$\begin{align} \dfrac{q_b}{ d^{1.5}} &= \dfrac{Q_b}{B d^{1.5}} = \sqrt{\rho_{sw} g}q_{b*} \end{align}$

計算結果

tsc = 0.05
qbs1 = np.sqrt(rhosw * g) *10.0 *  (lts)**(2.5)  #Brown Eq.
qbs2 = np.sqrt(rhosw * g) *8.0 *  (lts-tsc)**(1.5) #MPM Eq.
Qbs1 = qbs1 * lB #Brown Eq.
Qbs2 = qbs2 * lB #MPM Eq.

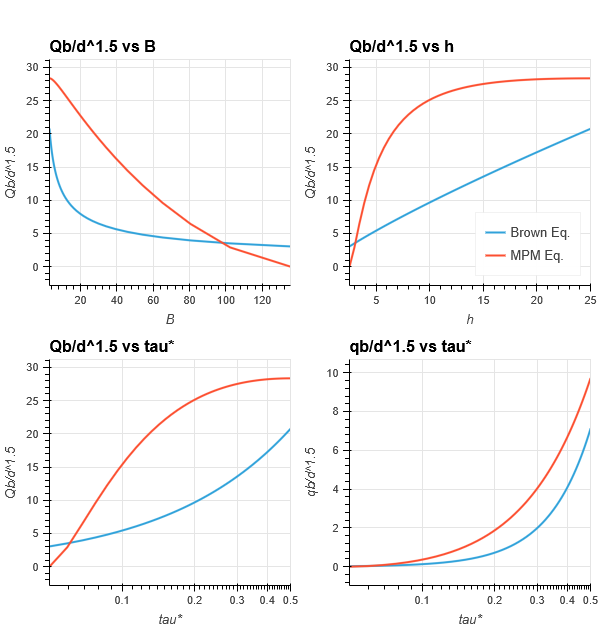
計算結果より、掃流砂量~川幅、掃流砂量~水深、川幅~水深の関係を次図に示します。

基準掃流砂量は、掃流砂量式によって変化の傾向が異なりますが川幅に対して単調減少、水深に対して単調増加を示しています。
無次元掃流力に対しても水深の関係と概ね同様ですが、Brown式は下に凸、MPM式は上に凸の形状を示しています。
当然ですが、単位幅流砂量は無次元掃流力に対して単調増加です。
本記事のテーマ「掃流砂量と川幅の関係について」は、「川幅の増加に対して流砂量は小さくなる」になります。
一方で、掃流砂量式の形によって水理量と掃流砂量の関係が異なる点についても留意する必要があります。

おまけ：MPM式（1.5乗則）の奇妙な特性

前述のMPM式において限界無次元掃流力がかなり小さい場合を想定して、限界無次元掃流力を0として同様の計算を行うと興味深い結果が得られます。計算結果は下図のとおりです。

不思議なことに、基準掃流砂量は先程と全く逆の特性を示し、川幅に対して単調増加、水深、無次元掃流力に対して単調減少となります。
この結果は、他2式との比較により間違った結果と考えられます。

この辺りの話は、掃流砂量式問題の本質だったりするので、私も上手く説明できないのですが、いくつも提案されている掃流砂量のいづれも不完全であることは言えると思います。

アプローチ方法は少し異なりますが、同様の内容について以下の論文で議論されています。

On A Reasonable, Functional Form for Bed-Load Formulas : Egashira Shinji, Robin K.Biswas, Harada Daisuke and Miyaamoto Kuniaki

39th IAHR World Congress 口頭発表

掃流砂量式については面白い話がたくさんあるので（ニーズは無さ過ぎますが）、気が向いたら書こうかなと。

掃流砂量式への粒径の影響
有効掃流力について
掃流砂量と浮遊砂量の関係

...etc

qbs1 = np.sqrt(rhosw * g) *10.0 *  (lts)**(2.5)  #Brown Eq.
tsc = 0.05
qbs2 = np.sqrt(rhosw * g) *8.0 *  (lts-tsc)**(1.5) #MPM Eq.
tsc = 0.0
qbs2d = np.sqrt(rhosw * g) *8.0 *  (lts-tsc)**(1.5) #MPM Eq.

Qbs1  = qbs1  *lB #Brown Eq.
Qbs2  = qbs2  *lB #MPM Eq.
Qbs2d = qbs2d *lB #MPM Eq.