流量時系列分布をガンマ分布で表現する理由 - 趣味で計算流砂水理 Computational Sediment Hydraulics for Fun Learning

以下の過去記事のアンサーです。

computational-sediment-hyd.hatenablog.jp

本記事はGitHub、nbviewer、Colabでも公開しています。

※Colabの解説記事はこちら

結論

石原先生の論文:流出函数による由良川洪水の解析に示されるとおりである。
論文中の「3.基礎式の解析」p.2までを以下に示す。

2.基礎方程式の誘導

貯留量 $S$ 、流入量 $I$ および流出量 $Q$ の連続式は、

$\begin{align} \dfrac{dS}{dt}=I-Q \end{align}$

である。

$S=Q/\alpha$ が成立するものとすると、

$\begin{align} \dfrac{dS}{dt}=\alpha\left(I-Q\right),\alpha>0 \end{align}$

さらに $f(t)=I/Q$ とすると、

$\begin{align} dQ=\alpha Q(f(t)-1) \end{align}$

となる。変数分離法により、この常微分方程式を解くと、

$\begin{align} \dfrac{dQ}{Q} &=\alpha(f(t)-1)dt \\ \int \dfrac{dQ}{Q} &= \int \alpha(f(t)-1)dt \\ \log Q &= \alpha \int f(t)dt - \alpha t + C \end{align}$

ここで、 $C$ ：積分定数である。流出量 $Q$ の式にすると、

$\begin{align} % Q&=\exp \left[-\alpha t + \alpha \int f(t) dt + C\right] \\ Q&=e^{-\alpha t + \alpha \int f(t) dt + C} \\ Q&=a e^{-\alpha t}e^{\alpha \int f(t)dt} \end{align}$

ここで、 $e^C$ を新たに $a$ とする。

次に $f(t)$ を設定する。

$t=0$ の時、 $Q=0$ となるためには、

$\begin{align} \int f(t) dt \rightarrow -\infty \end{align}$

$t=t_m$ (最大値を取る時刻)では、流入量 $I$ と流出量 $Q$ が等しくなるため、

$\begin{align} f(t_m)=I/Q=1 \end{align}$

となる。

このような関数形のうち、単純なものとして、 $f(t)=t_m/t$ を本論中では選択している。

$\begin{align} \int f(t)dt = \int t_m/t dt = t_m \log t +C \end{align}$

であるのでこれを代入すると、

$\begin{align} Q=ae^{-\alpha t} e^{\alpha \int f(t)dt} = a t^n e^{-\alpha t} \end{align}$

ここで、 $n=\alpha t_m$ ， $n \ge 1$

流域面積をBとすると比流量（単位流域面積当たりの流量）は、

$\begin{align} q=\dfrac{Q}{B}=\dfrac{a}{B}t^n e^{-\alpha t} = a_1 t^n e^{-\alpha t} \end{align}$

ここで、 $a_1=Q/B$ である。

3.基礎式の解析

次に、 $a_1$ を消去する。条件としては単位雨量に対して単位流出流量曲線（以下、論文図―2）を考える。

単位時間 $dT$ 当たり、単位雨量が降ったとする。 $q$ を時間に関して $0$ ～ $\infty$ まで積分すると、単位雨量 $1\cdot dT$ と等しくなる。

$\begin{align} \int_0^\infty q dt = \int_0^\infty a_1 t^n e^{-\alpha t}dt = a_1 \dfrac{\Gamma(n+1)}{\alpha^{n+1}} \end{align}$

ここで、ガンマ関数の関係である以下の式を用いた。

$\begin{align} \int_0^\infty s^{x-1} e^{-as}ds &= \Gamma(x)/a^x \\ a_1 \dfrac{\Gamma(n+1)}{\alpha^{n+1}} & =1\cdot dT \\ a_1 &= \dfrac{\alpha^{n+1}}{\Gamma(n+1)}dT \\ q &=a_1t^n e^{-\alpha t} = \dfrac{\alpha^{n+1}}{\Gamma(n+1)}e^{-\alpha t}t^n dT \end{align}$

となる。両辺の単位を合わせるために、係数 $0.2778(=1000/3600)$ を乗ずることで、式（9）となる。

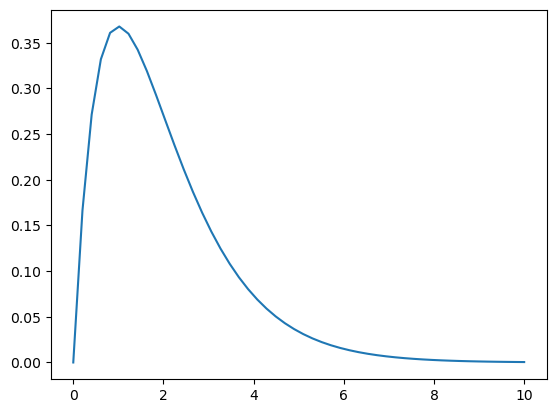
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gamma

x = np.linspace(0,10)
gamma_pdf = gamma(a=2.0, scale=1.0).pdf
y = gamma_pdf(x)

plt.plot(x,y)

GitHub

github.com

参考図書

リンク