最近科学技術計算を書いてなかったのでウォーミングアップにこんな感じの3次元キャビティー流れをSIMPLE法で書いてみました。

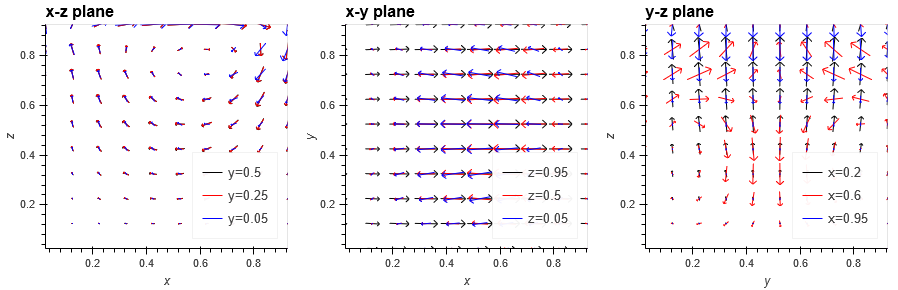
大きいものはこちら
はじめに
- SIMPLE法って複雑ですよね。そこで、pythonなら少しはわかりやすく書けるかと思いコードを書いてみました。
- 参考になるソースコードはないかとググったけど意外とヒットしなくて仕方なく一から書きました。
計算モデル
単純な3次元のキャビティー流れです。
計算条件
- 計算範囲は1 x 1 x 1の直方体
- dx=dy=dz=0.05、メッシュ数は20 x 20 x 20の8000メッシュ
- 計算スキームは、スタッガードスキームのSIMPLE法、移流項は一次風上
- 上面(z=max)以外はノンスリップ条件
- 上面(z=max)はx方向流速として1を与える
- 外力項は重力も含めて考慮しない
- 非定常項はキャンセル(定常場を求める)
- レイノルズ数は100
ソースコード
式の導出は以下を参照
computational-sediment-hyd.hatenablog.jp
仮の速度の計算式
- 3本の運動方程式をaxisで切り替えて1つの関数にしています。私の定番の書き方です。
- 収束計算は不足緩和で係数は標準値を採用。ここは厳密じゃなくても良い。
- 行数は150。運動方程式がこれだけで書けるのは立派だと思う。
- スタッガードスキームつらい。コロケートならもっとスッキリするはず。
def calupre(p,u,v,w,Vdir,Vbound,alphaU,dx,dy,dz,nu,axis): # x: axis = 0, y: axis = 1, z: axis = 2 zero = float(0.0) V0 = np.copy(Vdir) nx, ny, nz = p.shape ac = np.zeros_like(Vdir) axp = np.zeros_like(Vdir) axm = np.zeros_like(Vdir) ayp = np.zeros_like(Vdir) aym = np.zeros_like(Vdir) azp = np.zeros_like(Vdir) azm = np.zeros_like(Vdir) b = np.zeros_like(Vdir) act = np.zeros_like(Vdir) if axis == 0: xs, ys, zs = 1, 0, 0 xmb, xpb, ymb, ypb, zmb, zpb = -1, -1, 0, ny-1, 0, nz-1 elif axis == 1: xs, ys, zs = 0, 1, 0 xmb, xpb, ymb, ypb, zmb, zpb = 0, nx-1, -1, -1, 0, nz-1 elif axis == 2: xs, ys, zs = 0, 0, 1 xmb, xpb, ymb, ypb, zmb, zpb = 0, nx-1, 0, ny-1, -1, -1 for i in range(xs, nx): for j in range(ys, ny): for k in range(zs, nz): c = (i,j,k) if axis == 0: uhxp = 0.5*u[i,j,k] + 0.5*u[i+1,j,k] uhxm = 0.5*u[i,j,k] + 0.5*u[i-1,j,k] vhyp = 0.5*v[i,j+1,k] + 0.5*v[i-1,j+1,k] vhym = 0.5*v[i,j ,k] + 0.5*v[i-1,j ,k] whzp = 0.5*w[i,j,k+1] + 0.5*w[i-1,j,k+1] whzm = 0.5*w[i,j ,k] + 0.5*w[i-1,j,k] elif axis == 1: uhxp = 0.5*u[i+1,j,k] + 0.5*u[i+1,j-1,k] uhxm = 0.5*u[i,j,k] + 0.5*u[i,j-1,k] vhyp = 0.5*v[i,j,k] + 0.5*v[i,j+1,k] vhym = 0.5*v[i,j,k] + 0.5*v[i,j-1,k] whzp = 0.5*w[i,j,k+1] + 0.5*w[i,j-1,k+1] whzm = 0.5*w[i,j ,k] + 0.5*w[i,j-1,k] elif axis == 2: uhxp = 0.5*u[i+1,j,k] + 0.5*u[i+1,j,k-1] uhxm = 0.5*u[i,j,k] + 0.5*u[i,j,k-1] vhyp = 0.5*v[i,j+1,k] + 0.5*v[i,j+1,k-1] vhym = 0.5*v[i,j,k] + 0.5*v[i,j,k-1] whzp = 0.5*w[i,j,k] + 0.5*w[i,j,k+1] whzm = 0.5*w[i,j,k] + 0.5*w[i,j,k-1] axp[c] = (max([-uhxp,0.0]) + nu/dx)*dy*dz axm[c] = (max([ uhxm,0.0]) + nu/dx)*dy*dz ayp[c] = (max([-vhyp,0.0]) + nu/dy)*dx*dz aym[c] = (max([ vhym,0.0]) + nu/dy)*dx*dz azp[c] = (max([-whzp,0.0]) + nu/dz)*dx*dy azm[c] = (max([ whzm,0.0]) + nu/dz)*dx*dy ac[c] = axp[c]+axm[c]+ayp[c]+aym[c]+azp[c]+azm[c] if axis == 0: b[c] = -dy*dz*( p[i,j,k] - p[i-1,j,k] ) + (1.0 - alphaU)/alphaU * ac[c] * V0[c] elif axis == 1: b[c] = -dx*dz*( p[i,j,k] - p[i,j-1,k] ) + (1.0 - alphaU)/alphaU * ac[c] * V0[c] elif axis == 2: b[c] = -dx*dy*( p[i,j,k] - p[i,j,k-1] ) + (1.0 - alphaU)/alphaU * ac[c] * V0[c] ac[c] /= alphaU act[c] = ac[c] if i == xmb : ac[c] += axm[c] elif i == xpb : ac[c] += axp[c] if j == ymb : ac[c] += aym[c] elif j == ypb : ac[c] += ayp[c] if k == zmb : ac[c] += azm[c] elif k == zpb : ac[c] += azp[c] b[c] += 2.0*azp[c]*Vbound def sor(u): u0 = np.copy(u) # deep copy for i in range(xs, nx): for j in range(ys, ny): for k in range(zs, nz): c = (i,j,k) xp,xm,yp,ym,zp,zm = (i+1,j,k),(i-1,j,k),(i,j+1,k),(i,j-1,k),(i,j,k+1),(i,j,k-1) if i == xmb : uxp ,uxm = u0[xp], zero elif i == xpb : uxp ,uxm = zero, u0[xm] else: uxp ,uxm = u0[xp], u0[xm] if j == ymb : uyp ,uym = u0[yp], zero elif j == ypb : uyp ,uym = zero , u0[ym] else: uyp ,uym = u0[yp], u0[ym] if k == zmb : uzp, uzm = u0[zp], zero elif k == zpb : uzp, uzm = zero, u0[zm] else: uzp ,uzm = u0[zp], u0[zm] ut = (axp[c]*uxp + axm[c]*uxm \ + ayp[c]*uyp + aym[c]*uym \ + azp[c]*uzp + azm[c]*uzm + b[c])/ac[c] u0[c] = ut return u0 unew = np.copy(Vdir) # deep copy for _ in range(100): utmp = sor(unew) err = np.abs(unew - utmp).max() unew = np.copy(utmp) if err < 10**(-3) : break # print(err) return unew, act
圧力補正値の計算式
def caldp(p,u,v,w,acu,acv,acw,dx,dy,dz): zero = float(0.0) dp = np.zeros_like(p) ac = np.zeros_like(p) axp = np.zeros_like(p) axm = np.zeros_like(p) ayp = np.zeros_like(p) aym = np.zeros_like(p) azp = np.zeros_like(p) azm = np.zeros_like(p) b = np.zeros_like(p) nx, ny, nz = p.shape for i in range(nx): for j in range(ny): for k in range(nz): c = (i, j, k) axp[c] = zero if np.abs( acu[i+1,j, k ] ) < 10**(-8) else dy**2*dz**2/acu[i+1,j, k ] axm[c] = zero if np.abs( acu[i ,j, k ] ) < 10**(-8) else dy**2*dz**2/acu[i ,j, k ] ayp[c] = zero if np.abs( acv[i ,j+1,k ] ) < 10**(-8) else dx**2*dz**2/acv[i ,j+1,k ] aym[c] = zero if np.abs( acv[i ,j, k ] ) < 10**(-8) else dx**2*dz**2/acv[i ,j, k ] azp[c] = zero if np.abs( acw[i ,j, k+1] ) < 10**(-8) else dx**2*dy**2/acw[i ,j, k+1] azm[c] = zero if np.abs( acw[i ,j, k ] ) < 10**(-8) else dx**2*dy**2/acw[i ,j, k ] ac[c] = axp[c]+axm[c]+ayp[c]+aym[c]+azp[c]+azm[c] b[c] = - (u[i+1,j,k] - u[i,j,k])*dy*dz \ - (v[i,j+1,k] - v[i,j,k])*dx*dz \ - (w[i,j,k+1] - w[i,j,k])*dx*dy def sor(dp0, omega): p0 = np.copy(dp0) # deep copy for i in range(nx): for j in range(ny): for k in range(nz): c = (i,j,k) xp,xm,yp,ym,zp,zm = (i+1,j,k),(i-1,j,k),(i,j+1,k),(i,j-1,k),(i,j,k+1),(i,j,k-1) if i == 0: pxp ,pxm = p0[xp], zero elif i == nx-1: pxp ,pxm = zero, p0[xm] else: pxp ,pxm = p0[xp], p0[xm] if j == 0: pyp ,pym = p0[yp], zero elif j == ny-1: pyp ,pym = zero , p0[ym] else: pyp ,pym = p0[yp], p0[ym] if k == 0: pzp, pzm = p0[zp], zero elif k == nz-1: pzp, pzm = zero, p0[zm] else: pzp ,pzm = p0[zp], p0[zm] pt = (axp[c]*pxp + axm[c]*pxm \ + ayp[c]*pyp + aym[c]*pym \ + azp[c]*pzp + azm[c]*pzm + b[c])/ac[c] p0[c] += omega*(pt - p0[c]) # p0[c] = ut return p0 dpnew = np.copy(dp) # deep copy for nn in range(1000): dptmp = sor(dpnew, float(1.8)) err = np.abs(dpnew - dptmp).max() dpnew = np.copy(dptmp) if err < 10**(-6) : print('SOR N =', nn) break return dpnew
全体のループ
- 収束計算の係数は標準値を採用
def SIMPLE(p,u,v,w,Uslip,Vslip,alphaU,alphaP,dx,dy,dz,nu): zero = float(0.0) nx, ny, nz = p.shape for nn in range(1000): u, acu = calupre(p,u,v,w,u,Uslip,alphaU,dx,dy,dz,nu,axis=0) v, acv = calupre(p,u,v,w,v,Vslip,alphaU,dx,dy,dz,nu,axis=1) w, acw = calupre(p,u,v,w,w,zero,alphaU,dx,dy,dz ,nu,axis=2) dp = caldp(p,u,v,w,acu,acv,acw,dx,dy,dz) p += alphaP*dp unew = np.copy(u) # deep copy vnew = np.copy(v) # deep copy wnew = np.copy(w) # deep copy for i in range(nx): for j in range(ny): for k in range(nz): if i !=0 : unew[i,j,k] = u[i,j,k] + (dp[i-1,j,k] - dp[i,j,k])*dy*dz/acu[i,j,k] if j !=0 : vnew[i,j,k] = v[i,j,k] + (dp[i,j-1,k] - dp[i,j,k])*dx*dz/acv[i,j,k] if k !=0 : wnew[i,j,k] = w[i,j,k] + (dp[i,j,k-1] - dp[i,j,k])*dx*dy/acw[i,j,k] err = max([np.abs(unew - u).max(), np.abs(vnew - v).max(), np.abs(wnew - w).max()]) print('N', nn, 'error =', err) u = np.copy(unew) # deep copy v = np.copy(vnew) # deep copy w = np.copy(wnew) # deep copy if err < 10**(-6) : break return p,u,v,w
コード全体
結論(タイトルの回収とか)
- SIMPLE法の解法を理解していることを前提とするとpythonを使うことにより随分スッキリとコーディングできると思います。少なくともFortranやCのグローバル変数まみれのものよりはましだと思います。でも、やっぱりSIMPLE法は煩雑です。
- 連立一次方程式の解法の部分を関数化すればもっとスッキリする。
- ちなみに計算時間は私のノートPC(スペックはこちら)で10分程度。フル3Dの計算が、ノートPCで、スクリプト言語で、10分でできるっていい時代になりましたね。
SIMPLE法について思うこと
- SIMPLE法は、高速に定常解を求めることが可能であり、OpenFOAMに採用される等実務的な解法だと思う。
- 更に本領を発揮するのはコロケート格子や非構造格子の場合であり、Rhie and Chowの補間を用いることにより複雑な形状でも解析可能となる。 その場合、連立一次方程式の解法に非対称行列に適用可能なものを用いる必要がある。近年は共役勾配法ベースのもの(BiCGStab法とか)が一般的だと思う。 また、プログラミングとしてもオブジェクト指向に適している。
- 欠点は高次精度のスキームが使えないこと。乱流問題とかには向いてないのかな。もちろん矩形格子なら可能です。
- 非定常問題はPISO等もあるが基本的には向いてないのかな。でも、非定常問題で厳密な計算を行う機会は少ないのであまり考えなくてもいいかなと。
参考書籍
プログラミングは以下を参考にしました。
リンク
リンク
レンダリングについて
Holoviews
二次元の図はHoloviewsで書いてます。 ソースはこちら
関連記事
computational-sediment-hyd.hatenablog.jp
ParaView
三次元の図はParaViewで書きました。 XMLベースのvtk形式に関する覚書 - Qiita を参考にxmlベースのvtkを作成しました。 ソースはこちら
ParaView Glance
話題のParaView Glance(web版ParaView)でレンダリングしてみました。
以下のサイトを参考にParaViewで作った図をvtkjsでエクスポートしました。以下ではhtmlも作成していますが上手くいきませんでした。
描画はParaView Glanceにアクセスしてvtkjsファイル(サンプル)をロードするだけです。 手順をgif化しました。
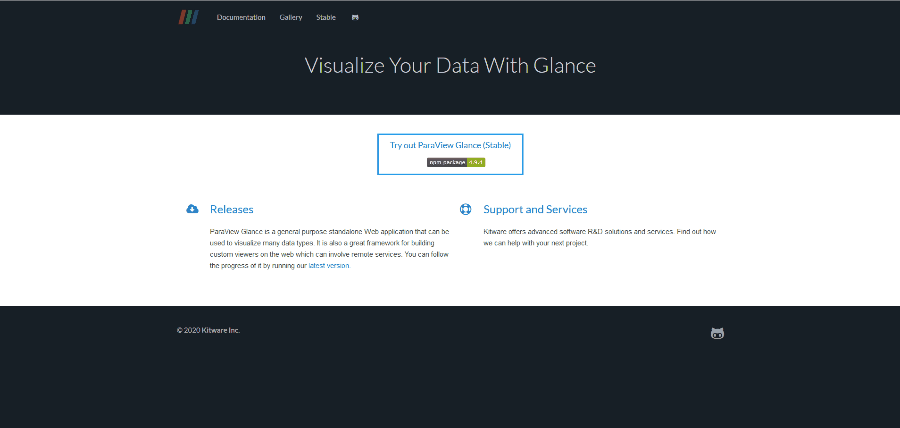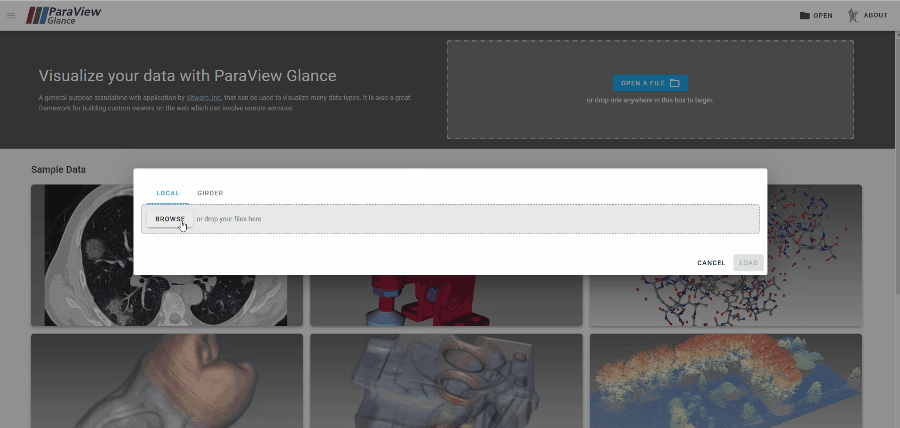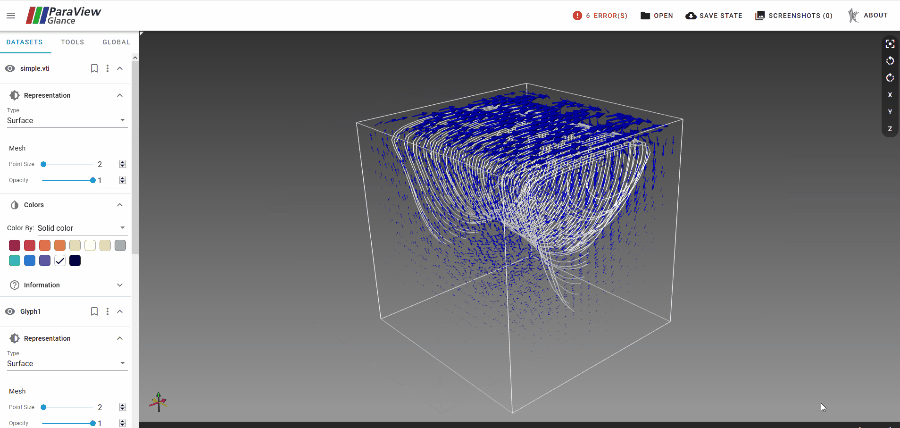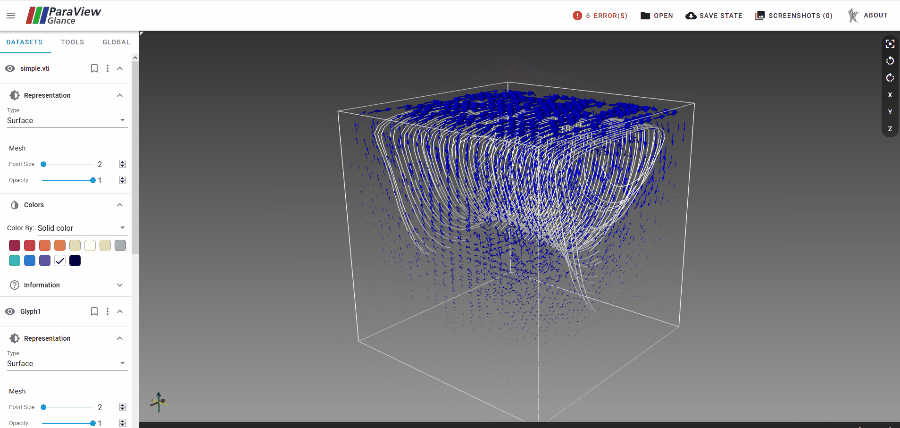
GitHub
おわりに
- 次はコロケート版を書こうかなと思ってます。
- その前に高速化の話を書くかも。
- 詳細な解説などリクエストがあればコメントをお願いします。
関連記事