備忘録：本間の越流公式について - 趣味で計算流砂水理 Computational Sediment Hydraulics for Fun Learning

たまには古典的な水理学の話でも。

概要
本間の越流公式
なぜ未だに多用されるのか
表記上の注意
GitHub
参考文献
関連記事

概要

本間の越流公式とは越流堤上下流の水位と通過流量の関係を示した実験式です。

以下の2報で発表されたのが最初であり、現在でも数値解析、設計などで現役バリバリで使われています。

本間の越流公式

越流堤上下流の水位と通過流量の関係を示した下式が本間の越流公式と呼ばれています。

本式では、上流側の流速（接近流速と呼ばれる）が0であることが条件となっています。接近流速が0でない場合の補正式も提案されています。（例えば、栗城の方法など。河川砂防技術基準　調査編第7章第3節－5参照)

$\begin{align} Q &= \left\{ \begin{array}{ll} m h_1 B \sqrt{2gh_1} & \left(\dfrac{h_2}{h_1} \lt \dfrac{2}{3}\right) : 完全越流\\ \dfrac{3\sqrt{3}}{2}m h_2 B \sqrt{2g(h_1-h_2)} & \left(\dfrac{h_2}{h_1} \geq \dfrac{2}{3}\right) : 潜り越流 \end{array} \right. \end{align}$

ここに、 $B$ :越流堤長、 $m$ :流量係数 $=\dfrac{2}{3}\sqrt{\dfrac{1}{3}} \mu$ 、 $\mu$ :遠心力による係数(1以下)、 $m$ は広幅の台形堰の場合、0.35程度となるため、通常 $m=0.35$ とすることがほとんどである。

出典：河川砂防技術基準　調査編第7章第3節－5

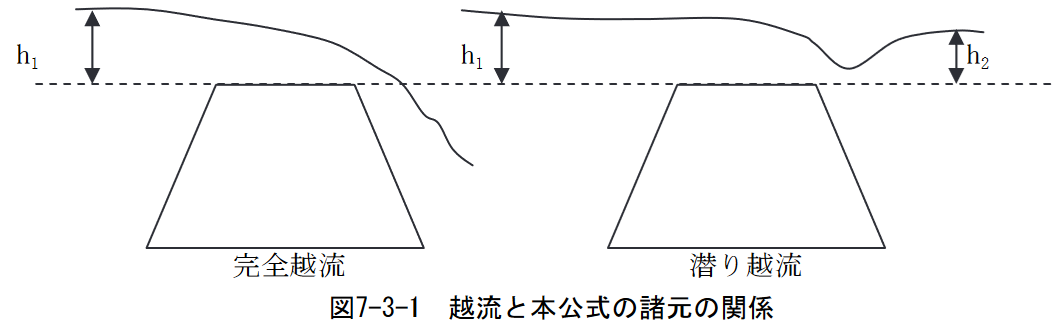
なぜ未だに多用されるのか

なぜこのような古典的な式が未だに多用されるかについて考えてみる。

元々は下図のように越流堤の背面（下流側）において射流や流れの剥離による渦などを厳密に計算することが難しいために、実験式が提案されています。

現在の計算技術では様々なモデルを組み合わせることによって一定精度で計算することは可能と考えられます。

一方で、河川流計算は浅水流近似式（Saint-Venantの式）を使用することがほとんどであり、それのみでは正確に計算することは難しいです。

そう考えると、越流堰近傍の厳密な流れ場の結果が必要になるケースはほとんどなく、概略の越流量が把握できれば良いため、この部分の計算にそれほど労力を割くメリットが無いことが本間の越流公式が未だに多用される要因と思われます。

ただし、近年では河川流計算の主流が横断面一次元から平面二次元に変わってきているため、本間の越流公式についても平面二次元計算に対応できるようなアップデートは必要と考えられます。

出典：本間仁：低溢流堰堤の流量係数（第一編）,1940

表記上の注意

本式には種々の表記方法がある。

最も多い事例は下式のとおり、2式それぞれに個別の流量係数があるかのような記載である。

$\begin{align} Q &= \left\{ \begin{array}{ll} m h_1 B \sqrt{2gh_1} & \left(\dfrac{h_2}{h_1} \lt \dfrac{2}{3}\right) : 完全越流\\ m' h_2 B \sqrt{2g(h_1-h_2)} & \left(\dfrac{h_2}{h_1} \geq \dfrac{2}{3}\right) : 潜り越流 \end{array} \right. \end{align}$

$m=0.35,m'=0.91$

例えば、河川砂防技術基準　調査編第7章第3節－5

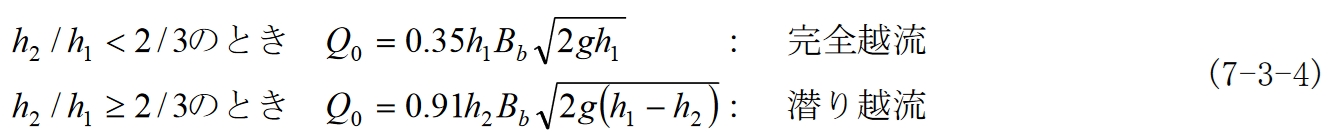
また、別の表記では下式のとおり流量係数を有次元の形式とすることもある。

$\begin{align} Q &= \left\{ \begin{array}{ll} C h_1 B \sqrt{h_1} & \left(\dfrac{h_2}{h_1} \lt \dfrac{2}{3}\right) : 完全越流\\ C' h_2 B \sqrt{(h_1-h_2)} & \left(\dfrac{h_2}{h_1} \geq \dfrac{2}{3}\right) : 潜り越流 \end{array} \right. \end{align}$