2024-01-19

河川技術者向け基礎講座　準二次元不等流計算3/4：一般断面の不等流計算2-分割断面法（平均流速公式レベル2）

教科書の「不等流計算」は理解できるが、実務で汎用される「準二次元不等流計算」がなかなか理解し難い方に向けて、記事を書きました。多分相当わかりやすいと思いますので、河川行政に関わる方やコンサルの方に読んで頂きたいです。

全4回の第3回目です。

本記事はGitHub、nbviewer、Colab、Marp（スライド形式）でも公開しています。

※Colabの解説記事はこちら

※Marpの解説記事はこちら

はじめに
基礎式
限界水深、等流水深の定義
- 等流水深
- 限界水深
離散化
数値計算方法
分割断面法の応用
分割断面法の必要性
横断面内の流速分布の実態
まとめ
断面特性を計算するプログラム例
不等流計算のプログラム例
参考文献
関連記事

はじめに

前回は一般断面で用いて断面内の流速が一様である条件での計算方法を示した。
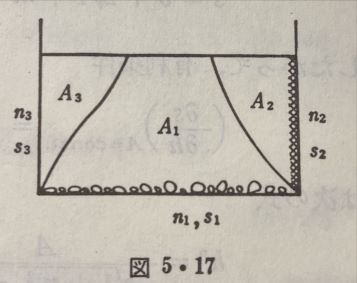
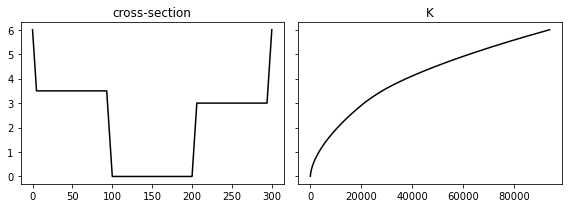
今回は下図の複断面形状（低水路+高水敷）にように、断面内の領域ごとに明らかな流速差が生じる場合の計算方法として分割断面法（平均流速公式レベル2）について説明を行なう。

分割断面とは、粗度が異なる領域ではなく、流速が異なる領域で区分する。分割断面内で粗度が一定である必要はない。
分割断面間で流れの干渉は生じないこと条件とする。
分割断面法において、
- 分割断面ごとに変わる：流速、河積、潤辺、粗度係数など
- 分割断面ごとに変わらない：水位、エネルギー勾配

基礎式

平均流速公式：マニング則

前回示した流速が一様の領域の平均流速公式は以下である。

$\begin{align} v &= \dfrac{1}{n'}i_e^{1/2}R^{2/3} \\ Q &= K i_e^{1/2} \\ K &\equiv \dfrac{A^{5/3}}{n'S^{2/3}} \\ n' &= \left( \dfrac{ \displaystyle \sum_{i=1}^{imax-1} S_i n_i^{3/2}}{ \displaystyle \sum_{i=1}^{imax-1} S_i } \right)^{2/3} \end{align}$

ここに、 $Q$ :流量、 $H$ ：水位、 $A$ ：河積、 $v$ ：流速、 $R=A/S$ ：径深、 $S$ ：潤辺、 $K$ ：通水能、 $n'$ ：マニングの粗度係数（合成粗度）とする。

分割断面法では、各分割領域で上式が成り立つことを条件に分割断面ごとの流量 $Q_n$ の総和が全体の流量 $Q$ として次式を導出する。

$\begin{align} Q &= \sum^{n} Q_n \\ &= \sum^{n} K_n i_e^{1/2} \\ K &\equiv \dfrac{A_n^{5/3}}{n_n'S_n^{2/3}} \\ \end{align}$

ここに、添字nは各分割断面の諸元を示す。

運動方程式の生成項が摩擦損失のみの場合、マニング則を用いると以下のとおりになる。

$\begin{align} \dfrac{\tau}{\rho g A} = \dfrac{Q^2}{\left(\displaystyle \sum^{n} K_n \right)^2} \end{align}$

運動方程式

分割断面法における不等流計算の運動方程式は次式を用いる。

$\begin{align} & \dfrac{d}{dx}\left( \frac{\beta Q^2}{2gA^2} + H \right) = -\dfrac{\tau}{\rho g A} \end{align}$

ここに、 $Q$ :流量、 $H$ ：水位、 $A=\sum A_n$ ：河積、 $\tau$ ：コントロールボリュームに作用する力、 $\beta$ ：運動量補正係数とする。

前回示した一般断面の運動方程式とほぼ同型である。新たに追加された $\beta$ ：運動量補正係数について詳述しておく。

運動量補正係数

運動量補正係数は運動方程式の導出過程で、断面積分を行う際に必要となる係数である。

断面平均流速 $V$ は局所流速 $u$ の積分で表すことができる。分割断面法では次式となる。

$\begin{align} & V = \dfrac{ \displaystyle \sum^n {u_n}A_n}{A} \end{align}$

一次元の運動方程式の導出過程で、 $\dfrac{ \displaystyle \sum^n {u_n^2}A_n}{A}$ が現れるが、分割断面下では次式は成立しない。

$\begin{align} \dfrac{ \displaystyle \sum^n {u_n^2}A_n}{A} \neq V^2 \end{align}$

そこで次のように示す。

$\begin{align} \dfrac{ \displaystyle \sum^n {u_n^2}A_n}{A} &= \beta V^2 \\ \beta &\equiv \dfrac{ \displaystyle \sum^n {u_n^2}A_n}{V^2 A} \end{align}$

このとき、 $\beta$ を運動量補正係数と定義する。

分割断面法の運動方程式では、運動量補正係数を考慮する必要がある。

エネルギー補正係数

同様に、エネルギー保存則においても、エネルギー補正係数 $\alpha$ が必要となる。

$\begin{align} \dfrac{d}{dx}\left( \dfrac{\alpha q^2}{2gh^2} + h + z_b \right) &= -i_e \end{align}$

一次元のエネルギー保存則の導出過程では、 $\dfrac{ \displaystyle \sum^n {u_n^3}A_n}{A}$ が現れるが、分割断面下では次式は成立しない。

$\begin{align} \dfrac{ \displaystyle \sum^n {u_n^3}A_n}{A} \neq V^3 \end{align}$

そこで次のように示す。

$\begin{align} \dfrac{ \displaystyle \sum^n {u_n^3}A_n}{A} &= \alpha V^3 \\ \alpha &\equiv \dfrac{ \displaystyle \sum^n {u_n^3}A_n}{V^3 A} \end{align}$

このとき、 $\alpha$ をエネルギー補正係数と定義する。

分割断面法のエネルギー保存則では、エネルギー補正係数を考慮する必要がある。

ここで、水面形方程式を整理すると次式となる。

$\begin{align} \dfrac{d}{dx}\left( \dfrac{\alpha q^2}{2gh^2} + h + z_b \right) &= -i_e \\ - \dfrac{\alpha q^2}{gh^3}\dfrac{dh}{dx} + \dfrac{dh}{dx} + \dfrac{d z_b}{dx} &= -i_e \\ \dfrac{dh}{dx} &= \dfrac{i_b -i_e }{ 1 - \dfrac{\alpha q^2}{gh^3}} \end{align}$

水面形方程式の分母に $\alpha$ が含まれるため、前々回の説明したとおり、限界水深を計算する式が変更される（詳細は後述）。

補足：井田法による合成径深

参照：井田:広巾員開水路の定常流-断面形の影響について（わかりづらいので読まなくても良いです）

ここで、分割断面法において水深の代替として用いることが多い井田法による合成径深について説明しておく。

分割断面法による平均流速は次式で示される。

$\begin{align} Q &= \left( \sum^{n} \dfrac{1}{n'_n}R_n^{2/3} A_n \right) i_e^{1/2} \end{align}$

断面全体においてもマニング則が成立するとして次式を定義する。

$\begin{align} Q &= \dfrac{1}{N}R^{2/3} i_e^{1/2} A \end{align}$

ここに、 $N$ ：断面全体のマニングの粗度係数、 $R$ ：断面全体の径深を示す。

2式を連立すると次式が導出される。

$\begin{align} R &= \left( \dfrac{N}{A} \sum^{n} \dfrac{1}{n'_n}R_n^{2/3} A_n \right)^{3/2} \end{align}$

本式からわかるとおり、径深 $R$ と粗度係数 $N$ は独立していない。

井田は、水理計算上取り扱いやすいように、径深 $R$ と粗度係数 $N$ は独立させるために、次式が成立する $N$ を $N_c$ と定義した。

$\begin{align} N_c \sum^{n} \dfrac{1}{n'_n}R_n^{2/3} A_n \equiv \sum^{n} R_n^{2/3} A_n \end{align}$

よって、

$\begin{align} N_c \equiv \dfrac{ \displaystyle \sum^{n} R_n^{2/3} A_n }{\displaystyle \sum^{n} \dfrac{1}{n'_n}R_n^{2/3} A_n} \end{align}$

これを元の $R$ の式に代入すると $R_c$ :井田法による合成径深が得られる。

$\begin{align} R_c &= \left( \dfrac { \displaystyle \sum^{n} R_n^{2/3} A_n }{A} \right)^{3/2} \end{align}$

$R_c$ は水位のみで決まるため、分割断面法において水深の代替として用いられることが多い。

※ $N_c$ は井田による等価粗度係数、合成粗度係数などと呼ばれる。前回定義した合成粗度係数と混同しないように注意すること。

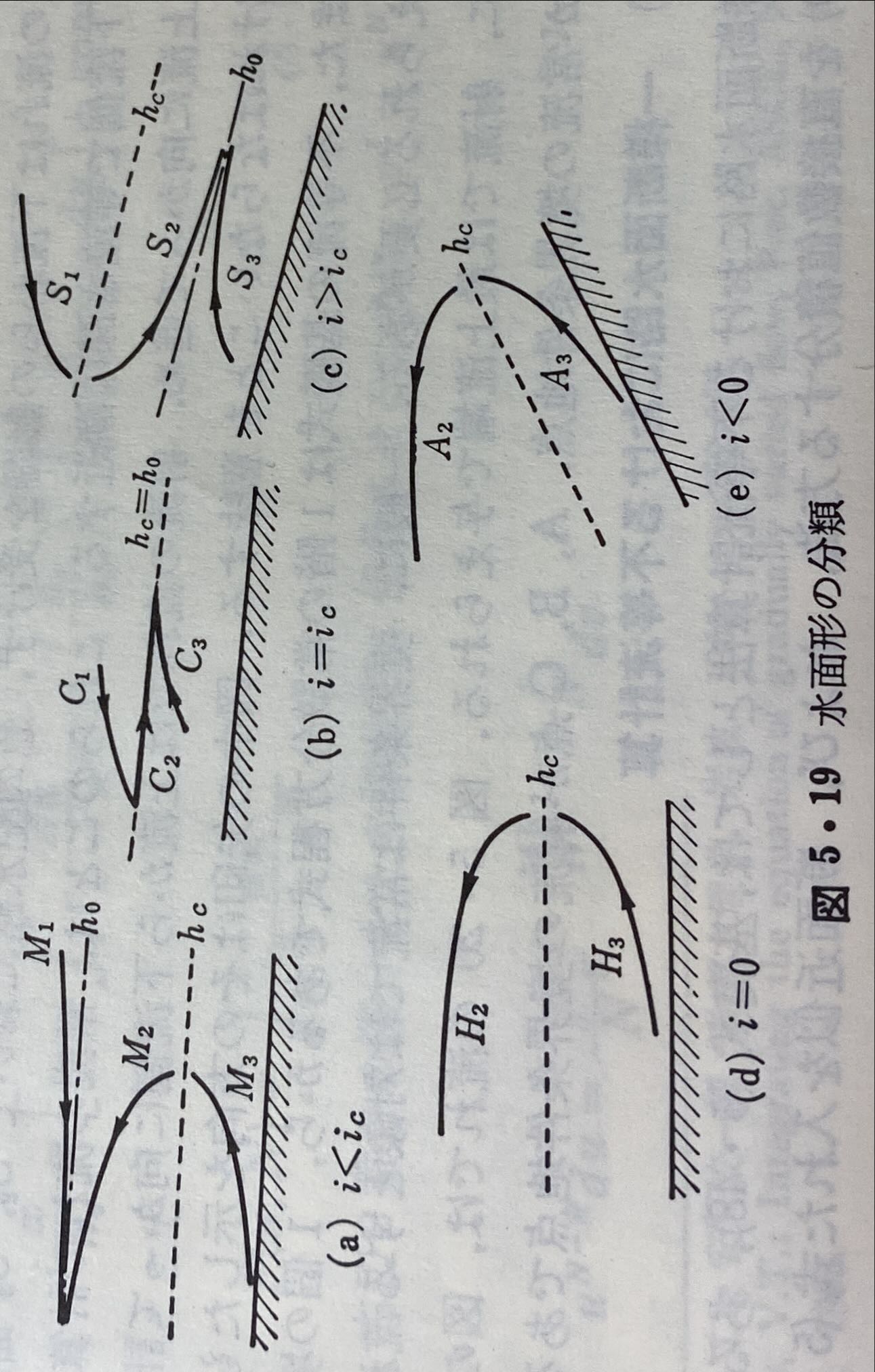
限界水深、等流水深の定義

一般断面の基礎式を用いて、限界水深、等流水深を矩形断面と同様に定義で設定することは難しいため、便宜的に以下のとおりに設定する。

等流水深

全ての損失による水頭の勾配が河床勾配 $i_b$ と釣り合う状態を等流と定義してその水深を等流水深とする。なお、一般断面では水深を用いないため、等流時の水位(以下、等流水位と定義)となる。

$\begin{align} \dfrac{\tau}{\rho g A} = i_b \end{align}$

生成項が摩擦損失のみの場合は、

$\begin{align} \dfrac{Q^2}{\left(\displaystyle \sum^{n} K_n \right)^2} = i_b \end{align}$

となり、これを満足する水位 $H$ を反復法などにより求めれば良い。

限界水深

フルード数が1となる水位を限界流時の水位(以下、限界水位と定義)とする。

フルード数はエネルギー保存則の分母が0より、

$\begin{align} 1 &= \dfrac{\alpha q^2}{gh^3} \\ Fr&= \dfrac{V}{ \sqrt{\dfrac{gh}{\alpha}}} \\ Fr&= \dfrac{Q}{A\sqrt{\dfrac{gh}{\alpha}} } \end{align}$

となるが、平方根の中に水深 $h$ が含まれるため、一般断面ではそのままでは計算できない。

そのため、分割断面法では水深 $h$ の代替として井田の合成径深 $R_c$ を使用することが多い。その他には径深 $R=A/S$ 、 $A/B$ を用いることもある。

参考：FORUM8ソフトウェア：等流・不等流の計算・3DCAD Ver.9 Q&A

離散化

離散化は次式となる。なお、 $i$ :上流側、 $i-1$ :下流側とする。

$\begin{align} \left(\frac{\beta_i Q^2}{2gA^2_i} + H_i \right) -\left( \frac{\beta_{i-1} Q^2}{2gA_{i-1}^2} + H_{i-1} \right) &= \dfrac{1}{2}\left(\dfrac{Q^2}{K_i^2} + \dfrac{Q^2}{K_{i-1}^{2}}\right)\Delta x \\ A&=\sum A_n \\ K&=\sum K_n \end{align}$

常流の場合、下流から逐次計算を行なうため未知数は $H_i$ のみとなる。

数値計算方法

一般断面の場合、離散式の未知数 $H_i$ による微分が難しいため、ニュートン法が使いづらい。そのため、二分法を使用することをおすすめする（もちろんニュートン法を使っても良い)。ただし、通常の二分法では安定的に計算することが難しいため、少し工夫が必要である。

分割断面法の応用

分割断面法では流速の異なる領域ごとに分割断面を設けるため、高水敷と低水路という区分に限らない。例えば、横断面内に樹林帯が存在し、著しく流速が低下する場合などはその領域に分割断面を設定しても良い。

import matplotlib.pyplot as plt
x=[0, 5,93,100,200,206,294,300]
y=[6, 3.5, 3.5,  0,  0,  3,  3,  6]
plt.plot(x,y, c='k')
plt.vlines([0,93,206,300], ymin=0, ymax=6, color='r')
plt.axvspan(xmin=30, xmax=60)
plt.show()                # 描画

png

分割断面法の必要性

なぜ分割断面法が必要性なのか？合成粗度による方法では駄目なのか?について考える。
基礎式をふまえて正しく積分するという意味は当然ある。
複断面河道の流れを適切に一次元で取り扱うこと自体に相当無理がある。
それでも、分割断面法を使う理由は河床抵抗を適切な評価できることである。
次図に水位と通水能の関係を示すが、合成粗度では高水敷付近で不連続となるが、分割断面法では解消されている。これにより、安定的に水理計算が可能となる。

合成粗度
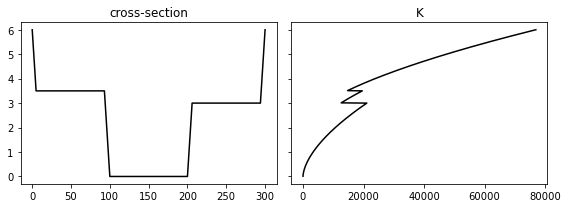
分割断面法

少し考えてみよう。

下に多自然川づくりの例でよく見る横浜市のいたち川の写真を示す。写真の下（施工後）の場合、どのように水理計算を行えば良いと思いますか？

合成粗度？分割断面法？

出典：（財）リバーフロント整備センター「多自然川づくり参考事例集」https://tenbou.nies.go.jp/science/description/detail.php?id=95

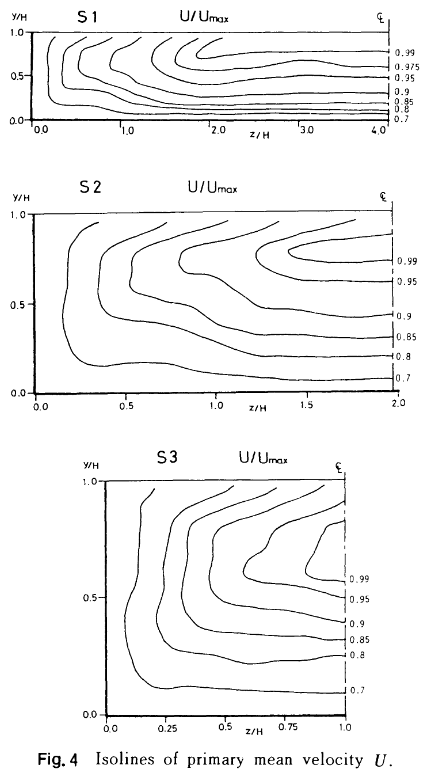
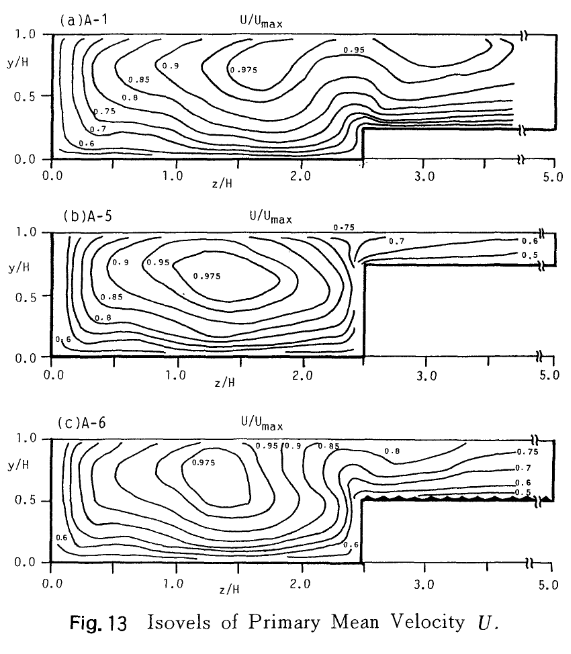
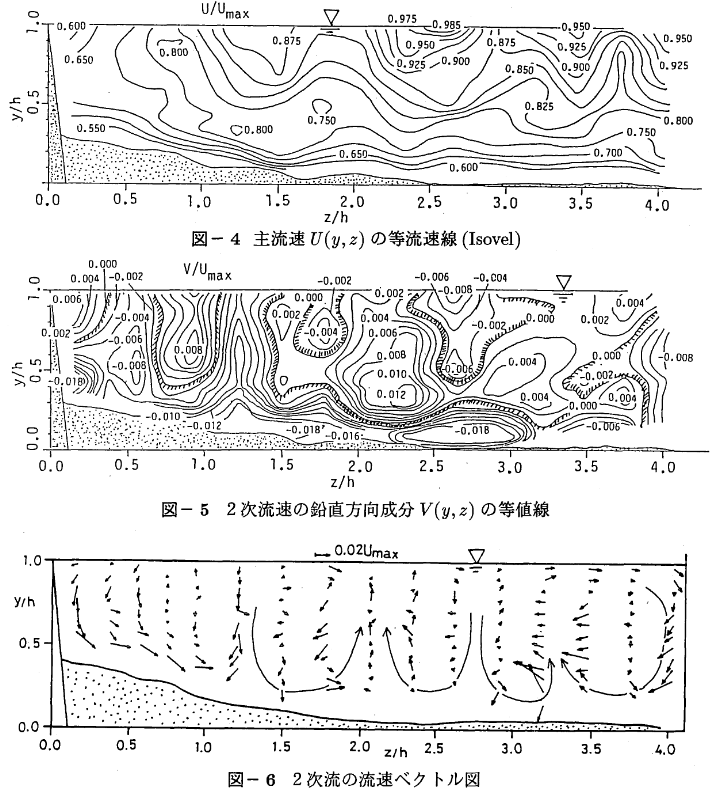
横断面内の流速分布の実態

実験水路の計測結果を参照すると、横断面内の流速分布は水路幅と水深の比（アスペクト比）によって次図のようになる。
流速分布は横断方法、鉛直方向の流れ(二次流：主流の数%程度の流れ）で大きさ決まる。
現地スケールで、特に出水時の観測事例はほとんどない。
アスペクト比が小さい断面形状では、Velocity dipと呼ばれる最大流速位置が水面より少し下に沈むような現象が生じる。

冨永ら1985

冨永ら1990

禰津ら1993

まとめ

流速の異なる複数の領域を持つ河道横断形状を対象とした一次元(準二次元)不等流計算方法について説明を行った。

一次元(準二次元)開水路流れの水理計算を行なう上ではここまで理解できれば十分。
逆に、不等流計算に限らず、一次元不定流計算、一次元河床変動計算などで水位を正確に計算したい場合は、ここまでは考慮して欲しい。
県管理河川の河道計画ではこれ以上の知識は不要。
次回以降説明する平均流速レベル3は、直轄管理河川の河道計画に特化した方法で他で使うことほぼ無い。

断面特性を計算するプログラム例

ボリュームがあるため、別ページに作成

不等流計算のプログラム例

Coming soon.

参考文献

リンク

jupyterをはてブロのmarkdownに変換

computational-sediment-hyd.hatenablog.jp

2024-01-08

勉強会の議事メモ：2024/01/08

勉強会お疲れ様でした。

一般座標系平面二次元河床変動計算を書く

computational-sediment-hyd.hatenablog.jp

上記記事のパターン1をベースに検討を進める。

小さなメッシュサイズおける浅水流計算の問題

computational-sediment-hyd.hatenablog.jp

状況を共有。圧力項と重力項の分離等の対応方法を検討。

四分木法

AMR法（Adaptive Mesh Refinement、適合格子細分化法）も含めて、関連資料の収集を行う。特に、2wayのやりとりについて離散化、コーディングも含めて収集する。

2024-01-06

河川技術者向け基礎講座　準二次元不等流計算2/4：一般断面の不等流計算

全4回の第2回目です。

本記事はGitHub、nbviewer、Colab、Marp（スライド形式）でも公開しています。

※Colabの解説記事はこちら

※Marpの解説記事はこちら

はじめに
基礎式
限界水深、等流水深の定義
- 等流水深
- 限界水深
離散化
数値計算方法
数値計算方法2：断面特性（河積、潤辺）の計算方法
数値計算方法3：（断面内の流速が一定と仮定した）合成粗度係数の計算方法
- 導出方法
断面特性を計算するプログラム例
不等流計算のプログラム例
参考文献
関連記事

はじめに

下図に示す実河川ような横断面形状は一般断面や自然河道断面などと呼ばれる。前回は矩形断面を対象として不等流計算を行ったが今回は一般断面を対象とする。
このような実務者向けの計算テクニックは水理公式集、河川砂防技術基準などに一部記述はあるのものの参考書籍が少ない。

import matplotlib.pyplot as plt
L=[0, 5,93,100,200,206,294,300]
Z=[6, 3.5, 3.5,  0,  0,  3,  3,  6]
plt.plot(L,Z, c='k')
plt.show()                # 描画

png

基礎式

一般断面の不等流計算の基礎式は次式を用いる。

$\begin{align} & \dfrac{d}{dx}\left( \frac{Q^2}{2gA^2} + H \right) = -\dfrac{\tau}{\rho g A} \end{align}$

ここに、 $Q$ :流量、 $H$ ：水位、 $A$ ：河積、 $\tau$ ：コントロールボリュームに作用する力とする。

前項で示した矩形断面の式と比較して以下の変更を行っている。

エネルギー保存則をベースとした式形としたが、一般断面の計算では摩擦損失以外の抵抗を考慮するため、運動量保存則をベースとした式形とした。それにより、右辺の生成項の式形が変更されている。
$h+z_b$ (圧力項+重力項)を $H$ に書き換えている。

後者について補足すると、例えば、下図のように、WL1、WL2と2つの水位が与えらた場合にそれぞれ $h,z_b$ は定義できるだろうか。それぞれの定義は難しい上に $z_b$ は水位によって変わることが理解できる。これが、一般断面の大きな特徴であり、水位によって理論的な（物理的に意味を持つ）河床高が変わる。 $h,z_b$ の2変数を同時に解くことはできないため、 $h+z_b \equiv H$ として $H$ のみを変数として計算を行なう。

import matplotlib.pyplot as plt
x=[0, 5,93,100,200,206,294,300]
y=[6, 3.5, 3.5,  0,  0,  3,  3,  6]
plt.plot(x,y,c='k')
plt.axhline(y=5,c='b',label='WL1')
plt.axhline(y=3.3,c='b',ls='dashed',label='WL2')
plt.legend()
plt.show()                # 描画

png

マニング則についても以下のとおり若干の変更を加える。

$\begin{align} v &= \dfrac{1}{n}i_e^{1/2}R^{2/3} \\ Q &= \dfrac{1}{n}i_e^{1/2}\dfrac{A^{5/3}}{S^{2/3}} \\ Q &= K i_e^{1/2} \\ K &\equiv \dfrac{A^{5/3}}{nS^{2/3}} \end{align}$

ここに、 $Q$ :流量、 $H$ ：水位、 $A$ ：河積、 $v$ ：流速、 $R=A/S$ ：径深、 $S$ ：潤辺、 $K$ ：通水能、 $n$ ：マニングの粗度係数とする。

水位 $A$ 、潤辺 $S$ 、粗度係数 $n$ は、水位 $H$ の関数となる。式の簡略化のため、これらを合わせた通水能 $K$ を用いることがある。

運動方程式の生成項が摩擦損失のみの場合、マニング則を用いると以下のとおりになる。

$\begin{align} \dfrac{\tau}{\rho g A} = \dfrac{Q^2}{K^2} \end{align}$

限界水深、等流水深の定義

一般断面の基礎式を用いて、限界水深、等流水深を矩形断面と同様に定義で設定することは難しいため、便宜的に以下のとおりに設定する。

等流水深

全ての損失による水頭の勾配が河床勾配 $i_b$ と釣り合う状態を等流と定義してその水深を等流水深とする。なお、一般断面では水深を用いないため、正確には等流時の水位（以降、等流水位と定義）となる。

$\begin{align} \dfrac{\tau}{\rho g A} = i_b \end{align}$

生成項が摩擦損失のみの場合は、

$\begin{align} \dfrac{Q^2}{K^2} = i_b \end{align}$

となり、これを満足する水位 $H$ を反復法などにより求めれば良い。

限界水深

フルード数が1となる水位を限界流時の水位（以降、限界水位と定義）とする。

フルード数は、

$\begin{align} Fr = \dfrac{Q}{A\sqrt{gh}} \end{align}$

となるが、平方根の中に水深 $h$ が含まれるため、そのままでは計算できない。

そのため、水深 $h$ の代替として径深 $R=A/S$ を使用することが多い。その他には $A/B$ を用いることもある。

参考：FORUM8ソフトウェア：等流・不等流の計算・3DCAD Ver.9 Q&A

離散化

離散化は次式となる。なお、 $i$ :上流側、 $i-1$ :下流側とする。

$\begin{align} \left(\frac{Q^2}{2gA^2_i} + H_i \right) -\left( \frac{Q^2}{2gA_{i-1}^2} + H_{i-1} \right) = \dfrac{1}{2}\left(\dfrac{Q^2}{K_i^2} + \dfrac{Q^2}{K_{i-1}^{2}}\right)\Delta x \end{align}$

常流の場合、下流から逐次計算を行なうため未知数は $H_i$ のみとなる。

数値計算方法

一般断面の場合、離散式の未知数 $H_i$ による微分が難しいため、ニュートン法が使いづらい。そのため、二分法を使用することをおすすめする（もちろんニュートン法を使っても良い)。ただし、通常の二分法では安定的に計算することが難しいため、少し工夫が必要である。この点については次回詳述する。

数値計算方法2：断面特性（河積、潤辺）の計算方法

河道断面の座標を次図のように定義する。

河積 $A$ ,潤辺 $S$ ,径深 $R$ は次式で計算する。

$\begin{align} S_i &= \sqrt{(L_{i+1}-L_i)^2 + (Z_{i+1}-Z_i)^2} \\ A_i &= \left[H-0.5(Z_{i+1}+Z_i)\right](L_{i+1}-L_i) \\ S &= \sum_{i=1}^{imax-1} \!\! S_i \\ A &= \sum_{i=1}^{imax-1} \!\! A_i \\ R &= \dfrac{ A }{ S }\\ \end{align}$

ここでは、水際位置と座標定義点が同一であるが、実計算ではその限りではないため、水面と河道断面の交点を求めて計算する必要がある。詳細は後述するプログラムを参照いただきたい。

数値計算方法3：（断面内の流速が一定と仮定した）合成粗度係数の計算方法

ここまでは河道断面内で粗度係数が一定であることを前提としたが、上図のとおり、断面内で粗度係数が異なる場合について考える。

各潤辺の粗度の影響が及ぶ範囲を下図のように考えて、各領域の流速が $u_i$ が全て等しいと仮定する（Einsteinの方法）。その場合、断面平均流速 $V=u_i$ となる。断面全体および各潤辺領域でマニング則が成立すると仮定すると、次式が導出される。

出典：椿東一郎水理学1 pp.147

$\begin{align} n' &= \left( \dfrac{ \displaystyle \sum_{i=1}^{imax-1} S_i n_i^{3/2}}{ \displaystyle \sum_{i=1}^{imax-1} S_i } \right)^{2/3} \end{align}$

この方法は平均流速公式1a、 $n'$ は合成粗度係数と呼ばれる。

当然ではあるが水位によって合成粗度係数は変わる。

導出方法

断面全体の流速 $V$ が各領域の流速 $u_i$ と一致すると仮定する。(Einsteinの方法)

マニング則を用いると次式が導かれる。

$\begin{align} V &= u_i \\ \dfrac{1}{n'}\dfrac{A^{2/3}}{S^{2/3}} i_e^{1/2}&= \dfrac{1}{n_i}\dfrac{A_i^{2/3}}{S_i^{2/3}} i_e^{1/2}\\ \dfrac{1}{n'}\dfrac{A^{2/3}}{S^{2/3}} &= \dfrac{1}{n_i}\dfrac{A_i^{2/3}}{S_i^{2/3}} \\ \dfrac{1}{n'^{3/2}}\dfrac{A}{S} &= \dfrac{1}{n_i^{3/2}}\dfrac{A_i}{S_i} \\ A_i & = \dfrac{n_i^{3/2} S_i}{n'^{3/2} S }A \end{align}$

$A = \displaystyle \sum A_i, S = \displaystyle \sum S_i$ のため、

$\begin{align} A &= \displaystyle \sum A_i \\ &= \displaystyle \sum \dfrac{n_i^{3/2} S_i}{n'^{3/2} S }A \\ &= \dfrac{A}{n'^{3/2} S } \displaystyle \sum n_i^{3/2} S_i \\ n' &= \left( \dfrac{ \displaystyle \sum n_i^{3/2}S_i}{ \displaystyle \sum S_i } \right)^{2/3} \end{align}$

となり、合成粗度が導かれる。

断面特性を計算するプログラム例

ある河川断面の座標が次図のとおりとする。

import matplotlib.pyplot as plt
L=[0, 5,93,100,200,206,294,300]
Z=[6, 3.5, 3.5,  0,  0,  3,  3,  6]
plt.plot(L,Z, c='k')
plt.show()                # 描画

png

また、粗度係数は次のとおりとする。（個数は測点間で定義するためi-1個）

n=[0.041, 0.041,0.030,0.030,0.030,0.040,0.040]

断面特性を計算するプログラムは次のように記述できる。

def H2ABSKn(l, z, n, H):
    A, B, S, SN = float(0), float(0), float(0), float(0)
    
    for i in range(1, len(l)):
        dx = l[i] - l[i-1]    
        dy = z[i] - z[i-1]    
        hb, hf = H - z[i-1], H - z[i]
        
        if hb <= float(0) :
            if hf > float(0) :
                dx_dh = dx / (hf - hb)
                B += hf * dx_dh
                A += 0.5 * hf * hf * dx_dh
                Sp = hf * np.sqrt( dx_dh * dx_dh + 1.0)
                S +=  Sp
                SN += Sp * n[i-1]**1.5
        elif hf <= float(0) :
            if hb > float(0) :
                dx_dh = dx / (hf - hb)
                B -= hb * dx_dh
                A -= 0.5 * hb * hb * dx_dh
                Sp = hb * np.sqrt(dx_dh * dx_dh + 1.0)
                S += Sp
                SN += Sp * n[i-1]**1.5
        else :
            B += dx
            A += 0.5 * dx * (hf + hb)
            Sp = np.sqrt(dx**2 + dy**2)
            S += Sp
            SN += Sp * n[i-1]**1.5
            
    if S <= float(0):
        nd = float(0)
        K = float(0)
    else:
        nd = (SN/S)**(2.0/3.0)
        K = A**(5.0/3.0)/nd/S**(2.0/3.0)
        
    return A, B, S, K, nd

水位が5.0の場合、各種断面諸元は次のとおりとなる。

import numpy as np
A, B, S, K, nd = H2ABSKn(np.array(L), np.array(Z), np.array(n), 5.0)
print('河積：{}\n水面幅：{}\n潤辺：{}\n通水能：{}\n合成粗度係数：{}'.format(A, B, S, K, nd))

河積：858.0
水面幅：296.0
潤辺：298.3606797749979
通水能：47342.84520415623
合成粗度係数：0.03664910724429057

不等流計算のプログラム例

Coming soon.

参考文献

リンク

jupyterをはてブロのmarkdownに変換

computational-sediment-hyd.hatenablog.jp

2024-01-06

河川技術者向け基礎講座　準二次元不等流計算1/4：不等流計算の基礎

全4回の第1回目です。

本記事はGitHub、nbviewer、Colab、Marp（スライド形式）でも公開しています。

※Colabの解説記事はこちら

※Marpの解説記事はこちら

基礎式
離散化
水面形方程式
- 水面形の追跡方向
- 水面形の概形
数値計算方法
サンプルコード
補足：常流、射流混在流れの数値計算方法
参考文献
関連記事

基礎式

矩形近似した断面の不等流計算の基礎式はベルヌーイの式とマニング則より次式となる。

$\begin{align} & \dfrac{d}{dx}\left( \frac{q^2}{2gh^2} + h + z_b \right) = -i_e \\ & q = \dfrac{1}{n}i_e^{1/2}h^{5/3} \\ \end{align}$

ここに、 $q$ :単位幅流量、 $h$ ：水深、 $z_b$ ：河床高、 $i_e$ ：エネルギー勾配、 $n$ ：マニングの粗度係数、 $g$ ：重力加速度とする。

等流水深 $h_0$ 、限界水深 $h_c$ は次式となる。

$\begin{align} h_0&=\left(\dfrac{q^2n^2}{i_b}\right)^{3/10} \\ h_c&=\left(\dfrac{q^2}{g}\right)^{1/3} \end{align}$

ここに、 $i_b = - \dfrac{d z_b}{dx}$ ：河床勾配とする。

離散化

ベルヌーイの式とマニング則を連立させて離散化すると次式となる。なお、 $i$ :上流側、 $i-1$ :下流側とする。

$\begin{align} \left(\frac{q^2}{2gh^2_i} + h_i + {z_b}_i \right) -\left( \frac{q^2}{2gh_{i-1}^2} + h_{i-1} + {z_b}_{i-1} \right) = \dfrac{1}{2}\left(\dfrac{q^2n^2}{h_i^{10/3}} + \dfrac{q^2n^2}{h_{i-1}^{10/3}}\right)\Delta x \end{align}$

エネルギー勾配は上下流断面の平均値を用いている。

常流の場合、下流から逐次計算を行なうため未知数は $h_i$ のみとなる。

水面形方程式

前出のベルヌーイの式を変形して次の水面形方程式（水深の微分に関する方程式）を得る。

$\begin{align} \dfrac{d}{dx}\left( \dfrac{q^2}{2gh^2} + h + z_b \right) &= -i_e \\ - \dfrac{q^2}{gh^3}\dfrac{dh}{dx} + \dfrac{dh}{dx} + \dfrac{d z_b}{dx} &= -i_e \\ \dfrac{dh}{dx} &= \dfrac{i_b -i_e }{ 1 - \dfrac{q^2}{gh^3}} \\ &= \dfrac{i_b -i_e }{ 1 - {Fr}^2} \end{align}$

ここに、 $Fr = \dfrac{v}{\sqrt{gh}} = \dfrac{q}{\sqrt{gh^3}}$ ：フルード数とする。

水面形方程式の分子=0は $\dfrac{dh}{dx}=0$ のため等流状態を示し、前出の等流水深が得られる（等流水深の定義）。また、分母=0から限界水深が得られ（限界水深の定義）、 $\dfrac{dh}{dx}=\infty$ のため水面形が得られない。この地点は支配断面と呼ばれる。

上式を $h_0,h_c$ を用いて展開すると次式が得られる。（式展開は例えばここを参照）

$\begin{align} \dfrac{dh}{dx} &= i_b \dfrac{1-\left(\dfrac{h_0}{h}\right)^{10/3}}{1-\left(\dfrac{h_c}{h}\right)^3 } \end{align}$

不等流計算を行なう上で本式より以下を理解しておく必要がある。

水面形の追跡方向

$Fr \lt 1$ または $h_c \lt h$ または $v\lt\sqrt{gh}$ は、常流
$Fr \gt 1$ または $h_c \gt h$ または $v\gt\sqrt{gh}$ は、射流

と定義される。 $\sqrt{gh}$ は（微小振幅波理論による水面波の）波速であり、射流は $v\gt\sqrt{gh}$ のため水面変化が下流のみに影響するが、常流では上流にも影響をすることが示されている。そのため、不等流計算の水面形の追跡方向は、常流は下流から上流、射流は上流から下流となる。

水面形の概形

$h,h_0,h_c$ の関係より $\dfrac{dh}{dx}$ の符号が決まるため水面形の概形が把握できる。教科書にみられる緩勾配水路（M水路、 $h_0 \gt h_c$ ）や急勾配水路（S水路、 $h_0 \lt h_c$ ）などの水面形はこの考え方による描くことができる。

出典：椿東一郎水理学1 pp.151

数値計算方法

未知数 $h_i$ は直接計算できなため反復法によって近似解を求める。ここでは、ニュートン法を用いた。（参考：ニュートン法とは）

ニュートン法のアルゴリズムに沿うと、計算式は次のとおりとなる。

$\begin{align} f &= \left(\frac{q^2}{2gh^2_i} + h_i + {z_b}_i \right) -\left( \frac{q^2}{2gh_{i-1}^2} + h_{i-1} + {z_b}_{i-1} \right) - \dfrac{1}{2}\left(\dfrac{q^2n^2}{h_i^{10/3}} + \dfrac{q^2n^2}{h_{i-1}^{10/3}}\right)\Delta x \\ \dfrac{df}{dh_i} &= -\frac{q^2}{gh^3_i} + 1 + \dfrac{5}{3}\dfrac{q^2n^2}{h_i^{13/3}} \Delta x \end{align}$

$\begin{align} h^{new}_i &= h_i - \dfrac{f}{\dfrac{df}{dh_i}} % f &= \left(\frac{q^2}{2gh^2_i} + h_i + {z_b}_i \right) % -\left( \frac{q^2}{2gh_{i-1}^2} + h_{i-1} + {z_b}_{i-1} \right) % + \dfrac{1}{2}\left(\dfrac{q^2n^2}{h_i^{10/3}} + \dfrac{q^2n^2}{h_{i-1}^{10/3}}\right)\Delta x \\ % \dfrac{df}{dh_i} &= -\frac{q^2}{gh^3_i} + 1 % - \dfrac{5}{3}\dfrac{q^2n^2}{h_i^{13/3}} \Delta x \end{align}$

サンプルコード

単位幅流量0.5 $\mathrm{m^3/s/m}$ 、マニングの粗度係数0.02、河床勾配1/500、水路延長50 $\mathrm{m}$ の矩形水路を対象に下流端水位を限界水深としたときの水面形を計算せよ。なお、 $\Delta x$ は0.1 $\mathrm{m}$ とする。

import numpy as np

q = 0.5
n = 0.02
ib = 1/500
g = 9.8
dx = 0.1

h0 = (q**2*n**2/ib)**0.3 #等流水深
hc = (q**2/g)**(1/3) # 限界水深

L = np.arange(0,50.01,dx) #追加距離の配列
zb = L*ib #河床高の配列
h = np.zeros_like(L) #水深の配列

h[0] = hc #下流端条件
for i in range(1,len(h)):
    h[i] = h[i-1] #収束計算の初期値：一つ下流側の断面の水深
    f = 1.0 #仮値
    dfdh = 1.0 #仮値
    while np.abs(f/dfdh) > 10**(-8): # 反復計算の収束条件
        f = q**2/2.0/g/h[i]**2 + h[i] + zb[i] \
          -(q**2/2.0/g/h[i-1]**2 + h[i-1] + zb[i-1]) \
          - 0.5*(q**2*n**2/h[i]**(10/3) + q**2*n**2/h[i-1]**(10/3))*dx
        dfdh = -q**2/g/h[i]**3 + 1 + 5/3*q**2*n**2/h[i]**(13/3)*dx
        h[i] -= f/dfdh

import matplotlib.pyplot as plt

plt.plot(L,zb, label='zb')
plt.plot(L,h+zb, label='water level')
plt.plot(L,zb+h0, label='h0')
plt.plot(L,zb+hc, label='hc')
plt.legend()              # 凡例の表示
plt.show()                # 描画

補足：常流、射流混在流れの数値計算方法

実河川では射流が出現する範囲は局所的であり、射流の水面形が求めれることはそう多くない。

常流、射流の混在流れの計算方法については例えば以下が参考となる。

石川ら：常流・射流が混在する区間の不等流計算法(元論文が必要な方はDM下さい)
岡部ら：常流・射流の遷移を伴う不等流の数値計算法について
HEC-RAS River Analysis System - Hydraulic Reference Manual:Mixed Flow Regime Calculations（リンク切れの場合DM下さい）

かなり煩雑な計算が必要な上、わずかな条件の差で跳水位置が変わるなど実務的に取り扱いが難しい。また、射流部では $\Delta x$ を十分に小さくとることが必要となる。

実務では、常流区間の中で一部が射流であれば限界水深に置き換えて計算する場合が多い。また、射流部のフルード数が大きい場合は、次に示すようなリミッターを設定することにより水面形を滑らかにすることもある。

Fread et al.:An LPI Numerical Implicit Solution for Unsteady Mixed-Flow Simulation(元論文が必要な方はDM下さい)
MIKE 11 Reference Manua:Suppression of convective acceleration term（リンク切れの場合DM下さい）

計算負荷が大きくても問題がない場合は不定流計算による定常解により水面形を与える方法も考えられる。

常流、射流混在流れの水面形は計算手法によって大きく異なってしまうため、計算の際は十分に検討することが必要である。

参考文献

リンク

jupyterをはてブロのmarkdownに変換

computational-sediment-hyd.hatenablog.jp

2024-01-05

備忘録：Inkscapeのテキストの背景を着色する

基本的にベクタのデータに背景色というものはありません。背景を色で塗りたい場合はアートボードと同じ大きさの四角形を作ってそれを最背面に指定して色を塗ればそれが背景になります。

detail.chiebukuro.yahoo.co.jp

2023-12-31

（未解決）測量の高解像度を意識して、浅水流一次元計算でdxをかなり小さくすると上手くいかない件について

今年中に何とかしたかったのですが出来そうに案件です。

浅水流の計算（1D,2D共通）で、メッシュサイズを小さくしすぎると、ある閾値以下になると急に水位が大きくなると問題について、簡易なテストケースにより分析してみました。原因は未解明のままです。

放置しておくと厄介な問題になりそうな気がしています。

TL;DR

dxをどんどん小さくして0.5mとした場合に不定流計算の結果が怪しいっぽい
その原因は重力項？河床高+水深⇒水位として扱う影響か？
この問題は河床変動計算を行う場合、影響が大きいのでは？

モチベーション
河床縦断形状のモデル化
dxの差異による一次元計算結果の比較
各計算手法の差異
まとめ
GitHub
参考書籍
関連記事

モチベーション

近年、直轄管理河川では、河床の面的測量を順次実施されており、0.5～1.0m間隔の河床地形が得られる状況が整いつつあります。それに合わせて、計算格子をより小さくする必要があると考えられます。

そこで、平面二次元計算でメッシュサイズを小さくしていくとある閾値で急激に水位が上昇する結果が出たため、詳細について一次元で検証してみました。

河床縦断形状のモデル化

一次元計算のためのモデル地形を生成しました。 1/400の河床勾配に基本に、縦断方向に0.5m間隔の格子点を設けて、各点に-10～10cmの乱数を加算した以下の形状を想定しました。

全体図

拡大図

河床地形の生成
図化

dxの差異による一次元計算結果の比較

計算方法は過去記事と同様に、不等流計算、不定流計算（コロケート格子）、不定流計算（スタッガード格子）の3手法でテストしました。

3手法ともにdx=0.5、10、100mの3ケースの比較を行っています。dx=10、100mの河床地形は前述の0.5m間隔の格子点より縦断距離が一致する地点を抽出することにより作成しました。

なお、不定流計算では定常となるまで（実時間で3時間程度）繰り返し計算を行い、縦断的に流量が一定であることを確認している。

computational-sediment-hyd.hatenablog.jp

不等流計算

dx=0.5、10、100mの3ケースの平均的な水位は同程度であり、dxが小さいほど河床地形に応答して細かい水位変化が生じていることが分かる。

全体図

拡大図

不定流計算（コロケート格子）

dx=10、100mの2ケースと比較して、dx=0.5mの平均水位が0.2m程度大きくなっている。

全体図

拡大図

不定流計算（スタッガード格子）

dx=10、100mの2ケースと比較して、dx=0.5mの平均水位が0.1m程度大きくなっている。

全体図

拡大図

各計算手法の差異

dx=0.5mにおける3計算手法の水位を比較した。

水位は不等流<不定流：スタッガード<不定流：コロケートの順で大きくなっている。前項の結果を踏まえると、不定流の結果が真値からずれていると想定される。
不等流は、河床の凹凸に逆位相となるような常流の特徴を示しているが、不定流ではその特徴が見られない。
不定流：スタッガードは、河床の凹凸に対して訛ったような水面形を示している。
不定流：コロケートは、不等流と比較して、水面形が若干下流側に位相がずれるような形状となっている。
全体図

拡大図

計算
図化

まとめ

不定流計算では計算格子が小さくなると計算誤差が大きくなる傾向にある。一方、不等流計算ではその傾向は見られない。
その要因は不明であるが、重力項（河床勾配）の影響ではないかと思われる。
一般的にスキームチェックを行う場合、河床勾配はフラットで行うことが多いが、本記事のような急変地形でのテストも必要と考える。

GitHub

github.com

参考書籍

リンク

グラフの作成はHoloviewsを使用

computational-sediment-hyd.hatenablog.jp

はてブロへのhtmlグラフの埋め込み

computational-sediment-hyd.hatenablog.jp

jupyterをはてブロのmarkdownに変換

computational-sediment-hyd.hatenablog.jp

2023-12-30

祝：いつの間にかColabの標準ライブラリにholoviewsが追加されていました(2023-12-30)

いつの間にかGoogle Colaboratoryの標準ライブラリにholoviewsが追加されていました。

これでさらにholoviewsが使いやすいなります。

computational-sediment-hyd.hatenablog.jp

はじめに

基礎式

平均流速公式：マニング則

運動量補正係数

エネルギー補正係数

補足：井田法による合成径深

限界水深、等流水深の定義

等流水深

限界水深

離散化

数値計算方法

分割断面法の応用

分割断面法の必要性

横断面内の流速分布の実態

まとめ

断面特性を計算するプログラム例

不等流計算のプログラム例

参考文献

関連記事

一般座標系平面二次元河床変動計算を書く

小さなメッシュサイズおける浅水流計算の問題

四分木法

はじめに

基礎式

限界水深、等流水深の定義

等流水深

限界水深

離散化

数値計算方法

数値計算方法2：断面特性（河積、潤辺）の計算方法

数値計算方法3：（断面内の流速が一定と仮定した）合成粗度係数の計算方法

導出方法

断面特性を計算するプログラム例

不等流計算のプログラム例

参考文献

関連記事

基礎式

離散化

水面形方程式

水面形の追跡方向

水面形の概形

数値計算方法

サンプルコード

補足：常流、射流混在流れの数値計算方法

参考文献

関連記事

モチベーション

河床縦断形状のモデル化

dxの差異による一次元計算結果の比較

不等流計算

不定流計算（コロケート格子）

不定流計算（スタッガード格子）

各計算手法の差異

まとめ

参考書籍

関連記事