趣味で計算流砂水理 Computational Sediment Hydraulics for Fun Learning

computational-sediment-hyd.hatenablog.jp

上記過去記事のリバイスです。サンプルコードも追記したので参考にしていただけると良いかと思います。

潜水橋とは(Copilot)
「河道計画検討の手引き」における潜水橋に関する記述
計算式
計算プログラムの例
GitHub：一部のみ
関連記事

本記事のソースコードはGitHub、nbviewer、Colabでも公開しています。

※Colabの解説記事はこちら

潜水橋とは(Copilot)

潜水橋（せんすいきょう）とは、川の増水時に水面下に沈むことを前提として設計された橋のことです。英語では「submersible bridge」や「low-water bridge」とも呼ばれます。

特徴

欄干（らんかん）がない：流木やゴミが引っかからないようにするため。
構造がシンプル：水に沈んでも壊れにくいように、頑丈で低い構造。
水位が低いときだけ通行可能：増水時には通行止めになります。

利点

建設コストが安い。
洪水時に橋が流されにくい（沈むことで水の抵抗を減らす）。

欠点

増水時には通行できない。
夜間や悪天候時に危険が伴う。

日本での例

高知県の四万十川に多く見られ、「沈下橋（ちんかばし）」とも呼ばれます。
観光名所としても人気があります。

潜水橋は通常の河川を横過する橋梁と比べて小規模なものが多いと思います。

佐田沈下橋（四万十川）

出典：四万十川の沈下橋について - 四万十市公式ホームページ

流れ橋（上津屋橋）（木津川）

出典：流れ橋（上津屋橋）｜観光スポット｜お茶の京都｜京都府南部（山城地域）の観光情報

「河道計画検討の手引き」における潜水橋に関する記述

「河道計画検討の手引き」pp. 88～に計算式が示されておりますが、一部変なところがありますので修正しておきます。

計算式

潜水橋の下流断面1、上流断面2の両断面間の運動方程式は次のとおりになります。

$\begin{align} \dfrac{1}{2}\rho g {h_1} A_1 + \rho V_1 Q + D &= \dfrac{1}{2}\rho g {h_2} A_2 + \rho V_2 Q \\ \end{align}$

ここに、 $h$ :水深、 $A$ :断面積、 $V$ :流速、 $Q$ :流量、 $\rho$ :水の密度、 $g$ :重力加速度を示します。

$D$ は潜水橋の抵抗を示し、次のように定義されます。

$\begin{align} D &= \dfrac{1}{2}\rho C_d A_d V_2^2 \end{align}$

ここに、 $C_d$ :抵抗係数、 $A_d$ :潜水橋による流水断面に対する阻害面積を示します。

矩形近似（ $A=Bh$ ）、川幅一定として式展開すると、次のようになります。

$\begin{align} \dfrac{1}{2}\rho C_d A_d \dfrac{Q^2}{B^2h_2^2} &= \dfrac{1}{2}\rho gB({h_2}^2 - {h_1}^2) + \dfrac{\rho Q^2}{B}\left(\dfrac{1}{ h_2} - \dfrac{1}{ h_1}\right) \\ & = (h_2 - h_1)\left(\dfrac{1}{2}\rho gB({h_2} + {h_1}) - \dfrac{\rho Q^2}{B}\dfrac{1}{ h_2 h_1}\right) \\ C_d A_d &= (h_2 - h_1)\left( \dfrac{gB^3}{Q^2} h_2^2({h_2} + {h_1}) - 2 B\dfrac{h_2}{ h_1}\right) \end{align}$

さらに、水位上昇量 $\Delta h = h_2 - h_1$ とすると、次のように書き換えることができます。

$\begin{align} C_d A_d &= \Delta h \left( \dfrac{gB^3}{Q^2} (\Delta h + {h_1})^2(\Delta h + 2{h_1}) - 2 B \left( \dfrac{\Delta h }{ h_1}+1\right)\right) \\ \Delta h &= \dfrac{C_d A_d}{ \dfrac{gB^3}{Q^2} (\Delta h + {h_1})^2(\Delta h + 2{h_1}) - 2 B \left( \dfrac{\Delta h }{ h_1}+1\right)} \end{align}$

本式を反復法等により解くことで、潜水橋の水位上昇量 $\Delta h$ を求めることができます。

計算プログラムの例

基本プログラム

上記の計算式をPythonで実装した例を以下に示します。

import numpy as np
import matplotlib.pyplot as plt

def CalcDhLWB_sample1(Q, h1, B, Ad, Cd):
    g = 9.8  # Acceleration due to gravity in m/s^2
    errmax = 0.0001  # Maximum error tolerance
    max_iterations = 1000  # Maximum number of iterations
    dh = 0.0001 # Initial guess for delta H
    for _ in range( max_iterations):
        xx = Ad*Cd / ( g*B**3/Q**2*(dh+h1)**2*(dh+2.0*h1) - 2.0*B*(dh/h1+1) )
        if abs((xx - dh)/xx) < errmax:break
        dh = xx
    else:
        print("Calculation of low water bridge delta H does not converge")

    return xx

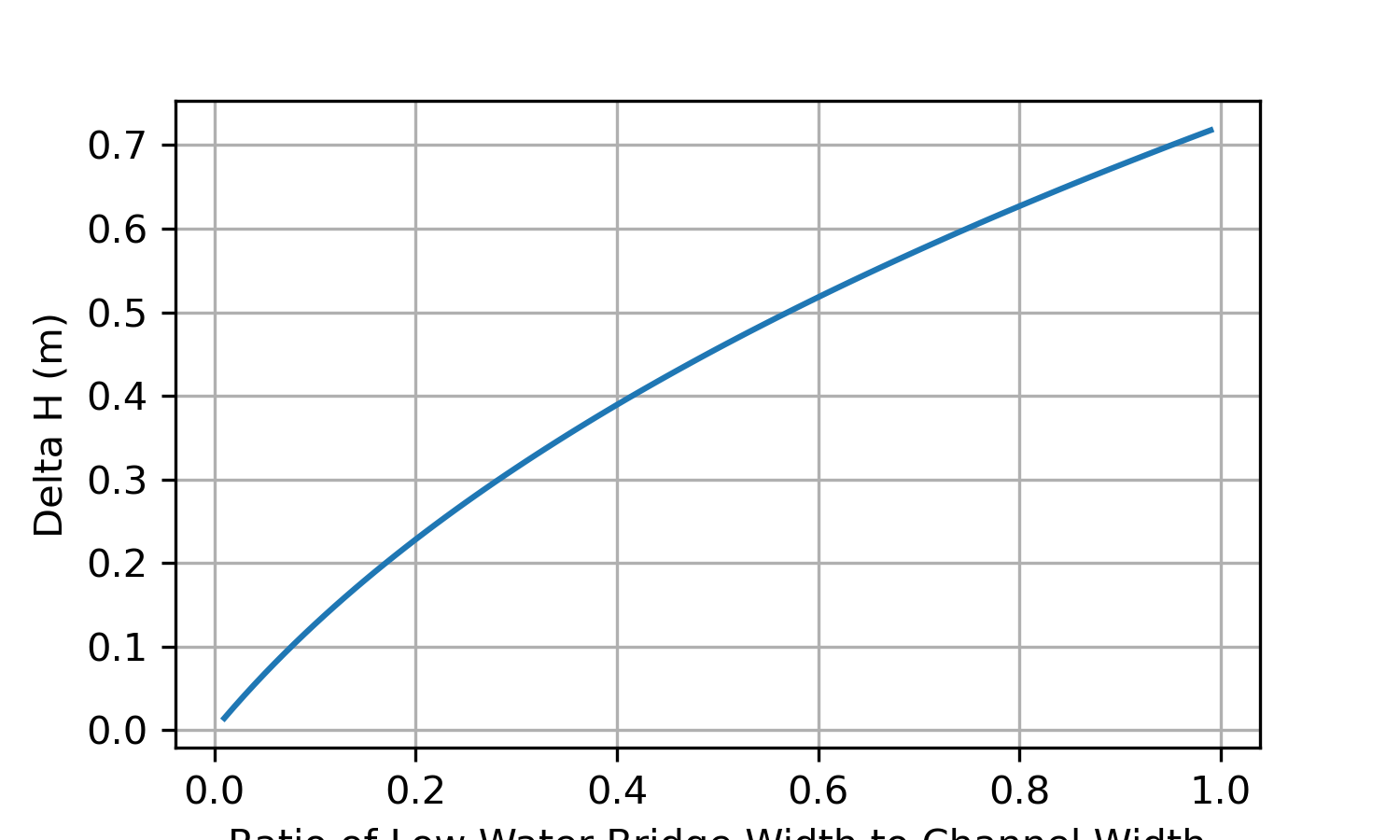
例えば、流量 $Q=1000$ m³/s、川幅 $B=100$ m、下流水深 $h_1=3$ m、抵抗係数 $C_d=1.6$ として、下流側の河積に対する阻害面積率と水位上昇量の関係を図化すると次のようになります。

h = 3
B = 100
Q = 1000
Cd = 1.6

ratio = np.arange(0.01, 1, 0.01)
ldh = [CalcDhLWB_sample1(Q, h, B, h*B*r, Cd) for r in ratio]

%matplotlib inline
fig, ax = plt.subplots(1, 1, figsize=(5, 3))
ax.plot(ratio, ldh, label='Low Water Bridge Delta H')
ax.set_xlabel('Ratio of Low Water Bridge Width to Channel Width')
ax.set_ylabel('Delta H (m)')
ax.grid()
plt.savefig('fig1.png', dpi=300)
plt.show()

png

射流時の処理の追加

射流条件下で上記ソースコードによる計算を行うと、水位上昇量 $h_2-h_1$ が負または解なしとなることがある。「河道計画検討の手引き」ではフルード数が0.6以上の時は水位上昇量は局所的になるため無視して良いとされているため、本計算を実施することは少ないかと思うが、念の為、エラー処理を追加しておく。

def CalcDhLWB_sample2(Q, h1, B, Ad, Cd):
    g = 9.8  # Acceleration due to gravity in m/s^2
    errmax = 0.0001  # Maximum error tolerance
    max_iterations = 1000  # Maximum number of iterations
    dh = 0.0001 # Initial guess for delta H
    for _ in range( max_iterations):
        xx = Ad*Cd / ( g*B**3/Q**2*(dh+h1)**2*(dh+2.0*h1) - 2.0*B*(dh/h1+1) )
        if abs((xx - dh)/xx) < errmax:break
        dh = xx
    else:
        print("Calculation of low water bridge delta H does not converge")
        xx = 0

    return xx if xx > 0 else 0.0

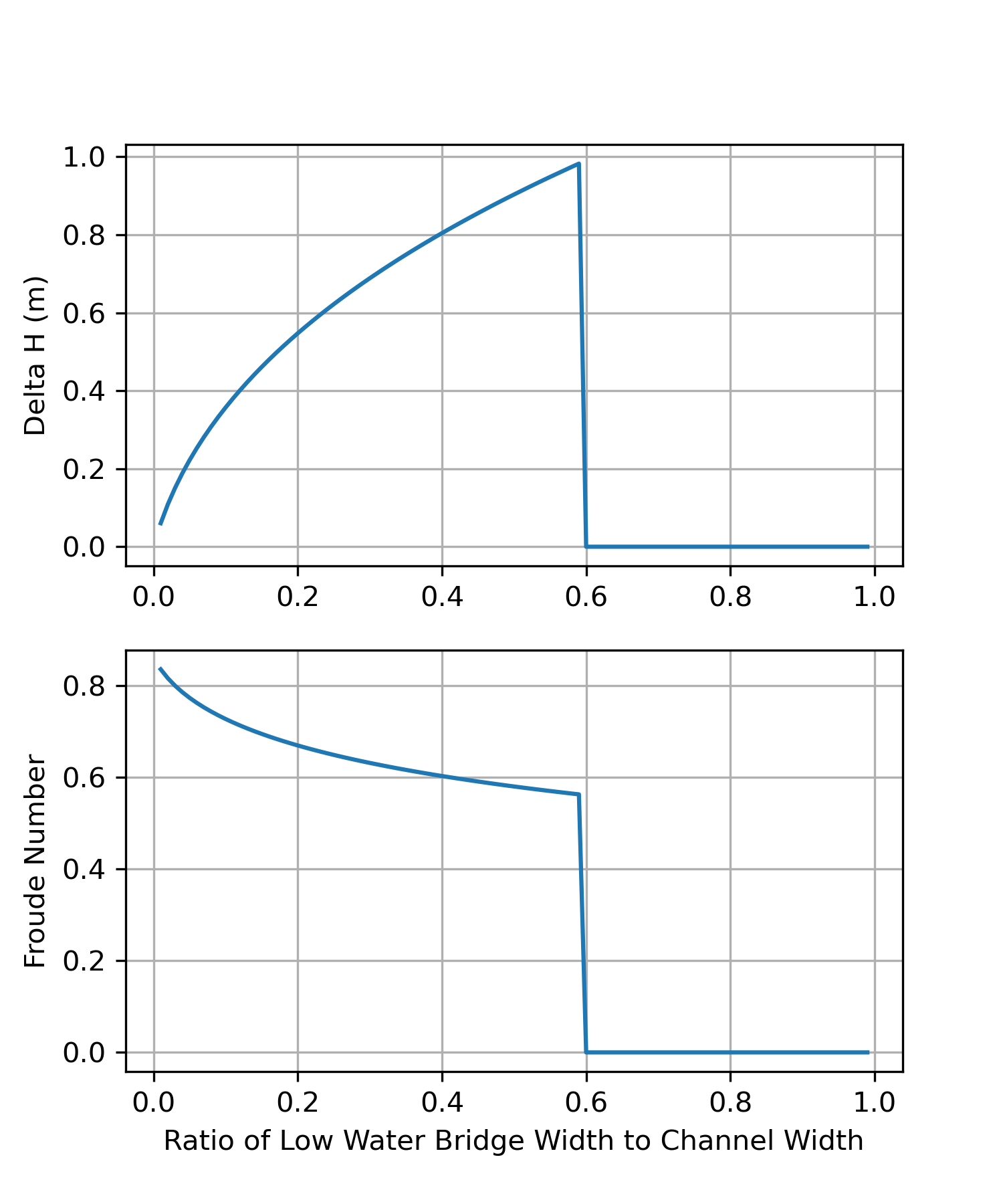
例えば、流量 $Q=1400$ m³/s、川幅 $B=100$ m、下流水深 $h_1=3$ m、抵抗係数 $C_d=1.6$ として、下流側の河積に対する阻害面積率と水位上昇量の関係を図化すると次のようになります。解なしについては0として図化している。参考として、潜水橋上流側のフルード数も図化している。なお、潜水橋下流側のフルード数は0.86となっている。

h = 3
B = 100
Q = 1400
Cd = 1.6

ratio = np.arange(0.01, 1, 0.01)
ldh = [CalcDhLWB_sample2(Q, h, B, h*B*r, Cd) for r in ratio]

ldh = np.array(ldh)
Fr2 = np.zeros_like(ldh)
Fr1 = Q/h/B/np.sqrt(9.8*h)
print("Froude number for normal flow:", Fr1)
for i, l in enumerate(ldh):
    if l > 0.0:
        Fr2[i] = Q/(l+h)/B/np.sqrt(9.8*(h+l))

%matplotlib inline
fig, ax = plt.subplots(2, 1, figsize=(5, 6))
ax[1].sharex = ax[0]

ax[0].plot(ratio, ldh, label='Low Water Bridge Delta H')
ax[1].plot(ratio, Fr2, label='Low Water Bridge Froude Number')
ax[1].set_xlabel('Ratio of Low Water Bridge Width to Channel Width')
ax[0].set_ylabel('Delta H (m)')
ax[1].set_ylabel('Froude Number')
ax[0].grid()
ax[1].grid()
plt.savefig('fig2.png', dpi=300)
plt.show()

png

自然河道断面（一般断面）への対応

厳密に計算する方法も考えられるがコードが煩雑になるため、水深の代わりに井田の合成径深を使うことでソースコードを変更せずに対応可能であり、ベターと考えます。

井田の合成径深の解説はこちら

GitHub：一部のみ

github.com