川幅 - 趣味で計算流砂水理 Computational Sediment Hydraulics for Fun Learning

久々に。。。

モチベーション

ひょんなことからTVD-MacCormack法を実装しようと思い、山地河川における河床変動の数値計算法（砂防学会の「急流河川の１次元河床変動（その２）」）を見て実装しようと思ったのですが、川幅に変化がある場合の計算が上手くいかなことを思い出したので少しまとめておきます。

基礎方程式

プリミティブ変数を通水断面積 $A$ と流量 $Q$ にした場合、連続式は次のようになるかと思います。

$\dfrac{\partial A}{\partial t} + \dfrac{\partial Q}{\partial x} = 0$

一方で運動方程式は、水面勾配を用いる場合と、河床勾配を用いる場合があります。ただし数式の表現は違いますが、同じものになります。前者と後者はそれぞれ次のようになります。

$\dfrac{\partial Q}{\partial t} + \dfrac{\partial }{\partial x}\left(\dfrac{Q^2}{A}\right) = -gA\left(\dfrac{\partial H}{\partial x} + I_e\right)$ ]

$\dfrac{\partial Q}{\partial t} + \dfrac{\partial }{\partial x} \left(\dfrac{Q^2}{A}+gI_1 \right) = -gA\left(\dfrac{\partial z}{\partial x} + I_e\right)+gI_2$

実河川への適用を考えると、前者の方が使いやすいですが、後者は所謂、保存系であり、システム系の方程式の解法（FDS、FVS、HLL系等）が使えます。この記事では前者を非保存系、後者を保存系と呼ぶことにします。何度も言いますが、数学的にこの二つの式は等価です。ただし離散化して解くと同じ答えにならない場合があります。

前者と後者を比較すると、後者では $I_1$ と $I_2$ が新たに現れています。 $gI_1$ は断面に働く静水圧、 $gI_2$ は川幅の変化とかサイドスロープの勾配の変化を表現する項になります。

多くの論文は単位幅だったり一様水路だったりするので、 $I_1$ は表現されているものの、 $I_2$ は矩形であれば0となるのでネグってることが多いです。次に数式でみてみます。

$I_1$ と $I_2$ の数式による表現

それぞれ表現すると次のようになります。

$gI_1 = g\int_0^{h}\left(h-\eta\right)bd\eta$

$gI_2 =g\int_0^{h}\left(h-\eta\right)\dfrac{\partial b}{\partial x}d\eta$

$b$ は流下距離 $x$ と河床から水面までの距離 $\eta$ の関数です。

$I_1$ は実河川でも求められますが、 $I_2$ はかなりめんどくさいです。ここでは矩形断面を想定し、河床から水面まで幅は一定( $=B$ )とします。

$gI_1 = gB\int_0^{h}\left(h-\eta\right)d\eta=gB\dfrac{h^2}{2}$

$gI_2 = g\dfrac{\partial B}{\partial x}\int_0^{h}\left(h-\eta\right)d\eta =g\dfrac{\partial B}{\partial x} \dfrac{h^2}{2}$

$I_2$ は一様水路の場合は0 $\left(\partial B/\partial x=0\right)$ になります。

ちなみに台形断面の場合は $I_2$ は比較的簡単に求められます。河床における川幅を $B_b$ 、サイドスロープの勾配を $S_L$ とすると $b(x,\eta)$ は次のように表現できます。

$b(x,\eta) = B_b + 2S_L \eta$

$gI_1 =g\int_0^{h}\left(h-\eta\right) \left(B_b + 2S_L \eta\right)d\eta = gB\dfrac{h^2}{2}+\dfrac{S_L}{3} h^3$

$gI_2 =g\int_0^{h}\left(h-\eta\right)\dfrac{\partial }{\partial x}\left(\dfrac{\partial B_b}{\partial x} + 2 \eta \dfrac{\partial S_L}{\partial x}\right)d\eta=g\dfrac{\partial B}{\partial x} \dfrac{h^2}{2} + \dfrac{h^3}{3} \dfrac{\partial S_L}{\partial x}$

「急流河川の１次元河床変動（その２）」の事例を記載の保存系の方程式で解く場合、 $I_2$ を考慮していないため再現できません。久々に解いたので忘れていたのもありますが、ここら辺の書き方がモヤッとしているため少し整理しようというのがモチベーションにつながっています。

保存系のシミュレーション

前述の「急流河川の１次現河床変動（その２）」の再現をしてみます。矩形の非一様断面の流れの解析です。運動方程式は次のようになります。

$\dfrac{\partial Q}{\partial t} + \dfrac{\partial }{\partial x} \left(\dfrac{Q^2}{A}+gB\dfrac{h^2}{2}\right) = -gA\left(\dfrac{\partial z}{\partial x} + I_e\right)+g\dfrac{\partial B}{\partial x} \dfrac{h^2}{2}$

連続式を再掲すると次の通りです。

$\dfrac{\partial A}{\partial t} + \dfrac{\partial Q}{\partial x} = 0$

これをTVD-MacCormack法で解いてみます。河川の解析では、Causon型が好まれているようですが、今回はGarciaのTVDを使ってみました。なお、Causonの原著を読んでいないので詳しくはわからないのですが、どうも任意に設定できるパラメータがあるようです。日本の河川の論文ではそのパラメータを0.5として表現している模様です。

え、なぜMacCormack法か？これは他のスキームと比較して明確でない！理由があります。

集中格子かつ等間隔のため、右辺の１階微分項を中央差分で解いた場合、[tex:(z{i+1} - z{i-1})/2\Delta x]となり $z_i$ が使われず気持ち悪い。
2Stepの場合、前進と後進をそれぞれ実施するため、上記の課題が克服できてるのではないか。

真面目に考えていないですが、こんな感じです。

TVD-MacCormack法

TVD-MacCormack法は連続式と運動方程式をベクトル表示して表現すると次のとおりです。

$\dfrac{\partial U}{\partial t} + \dfrac{\partial E}{\partial x} = S$

$U = \left(A,Q\right)^T$

$E = \left(Q,Q^2/A + gBh^2/2\right)$

$S = \left(0,-g\left(\partial z / \partial x +I_e + gh^2/2(\partial B /\partial x)\right)\right)$

GarciaのTVD-MacCormack法はCausonとは前進、後進が逆のようです。表現すると次のとおりです。

$U_i^{pred} = U_i - \dfrac{\Delta t}{\Delta x}\left(E_{i+1}^n - E_{i}^{n}\right) + \Delta t S_{i}^n$

$U_i^{corr} = U_i - \dfrac{\Delta t}{\Delta x}\left(E_{i+1}^{pred} - E_{i}^{pred}\right) + \Delta t S_{i}^{pred}$

$U_i^{ave} = \dfrac{U_i^{pred} + U_i^{corr}}{2}$

$U_i^{n+1} =U_i^{ave} + \dfrac{\Delta t}{\Delta x}\left(D_{i+1/2}^n-D_{i-1/2}^n\right)$

4行目の右辺第２項がTVD項になります。注意点は生成項 $S$ です。 $x$ に関する1階微分の項は予測子、修正子に合わせて前進、後進を使い分けています。

$D$ の求め方については書くのがだるいので、次を参考にしてください。 Roeの平均を使ってます。

Shallow Water Hydraulics

作者:Castro-Orgaz, Oscar,Hager, Willi H.
発売日: 2020/12/04
メディア: ペーパーバック

教えていただいたnumbaを使いました。当初は普通にfor文を使わずに書いてましたが、遅すぎたのでFortranチックにわざわざ書き換えてnumbaで高速化しました。

川幅の変化を考慮した結果

結果はこんな感じです。 Q=0.002m3/s、ks=0.018、下流端0.058mのケースを解いています。

f:id:SedimentHydraulics:20201101234856j:plain

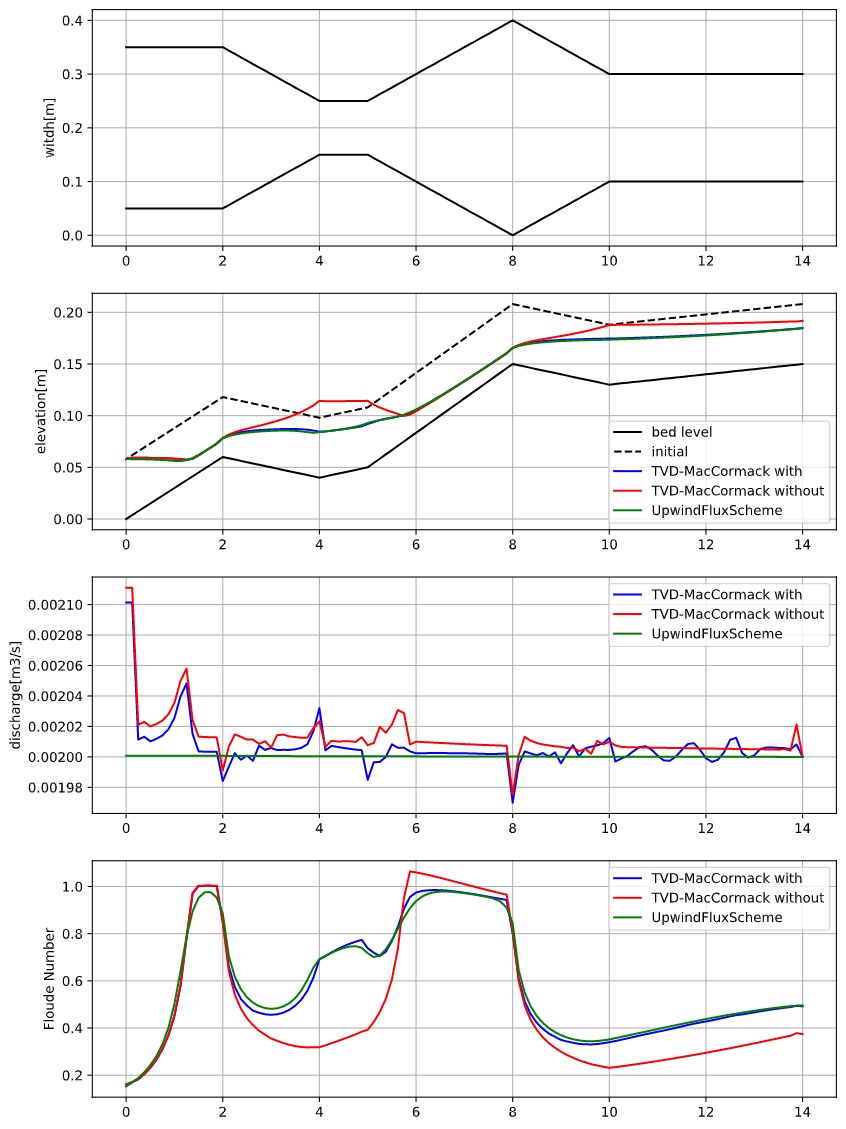
$I_2$ の項を考慮する、しないを比較してみました。当たり前といえば当たり前ですが・・・。

急拡、急縮の前後で水位を正しく表現できません。また幅を考慮していない場合、フルード数は1を超えています。元記事では水位のグラフのみしか示されていないのでなんとも言えませんが。

非保存系で解いた場合

非保存系でも解いてみました。保存系では集中格子で解いたので、千鳥格子にはせず、UpwindFluxSchemeを使いました。

TVD-MacCormackと似たような結果になります。

流量を比較すると保存系で解く場合はあまりよろしくありません。

結論

素直に非保存系を基礎方程式として解くのが良いのではないでしょうか？

論文等で１次元の洪水や河床変動解析においてFDSやHLL系等の保存系の基礎方程式を使って解いている場合、 $gI_2$ の川幅の変化をどう取り扱っているのかを確認した方が良いです。もちろん、現場のデータでは格子間隔が大きく（数十m〜200m程度）、川幅が大きく変わるようなデータにならない可能性はあり、川幅の影響を考慮しなくてもそれなりの結果となる場合もあるでしょうが。

あとは河床勾配の評価は難しいですね。

$I_2$ については、こうやって近似しよう、みたいな論文はみたことがありますが、実河川のデータでどの程度の近似精度があるのかはわかりません。

以上から、１次元の計算であれば、煩雑なスキームを使わずシンプルに解ける方が良いとの結論です。